Condition Decision Coverage criteria(CDC) for software testing

By: Prof. Dr. Fazal Rehman | Last updated: January 11, 2024

Example of Condition Decision Coverage  with 1 condition

C++

If(a > 7) { } else { }

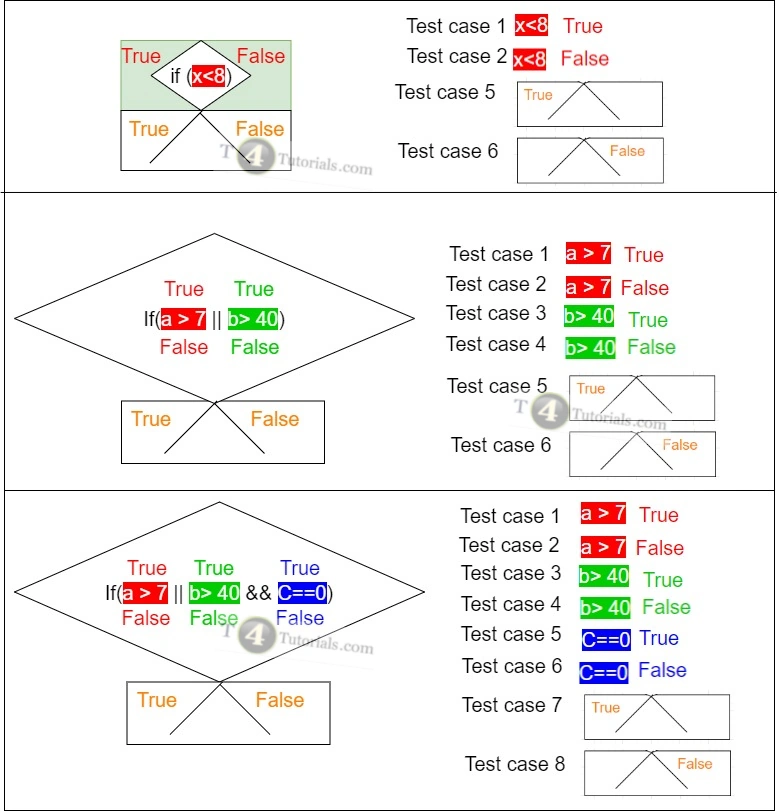
1 2 3 4 5 6

If(a > 7) { } else { }

Test Case ID	a > 7	Decision Outcome
1	True	Don’t care
2	False	Don’t care
5	Don’t care	True
6	Don’t care	False

Example of Condition Decision Coverage  with 2 conditions

C#

If(a > 7 || b> 40) { } else { }

1 2 3 4 5 6

If(a > 7 || b> 40) { } else { }

Test Case ID	a > 7	b> 40	Decision Outcome
1	True	Don’t care	Don’t care
2	False	Don’t care	Don’t care
3	Don’t care	True	Don’t care
4	Don’t care	False	Don’t care
5	Don’t care	Don’t care	True
6	Don’t care	Don’t care	False

Example of Condition Decision Coverage  with 3 conditions

C++

If(a > 7 || b> 40 && C==0) { } else { }

1 2 3 4 5 6

If(a > 7 || b> 40 && C==0) { } else { }

Test Case ID	a > 7	b> 40	C==0	Decision Outcome
1	True	Don’t care	Don’t care	Don’t care
2	False	Don’t care	Don’t care	Don’t care
3	Don’t care	True	Don’t care	Don’t care
4	Don’t care	False	Don’t care	Don’t care
5	Don’t care	Don’t care	True	Don’t care
6	Don’t care	Don’t care	False	Don’t care
7	Don’t care	Don’t care	Don’t care	True
8	Don’t care	Don’t care	Don’t care	False

 

---

More examples

C++

If(a > 4 && b >= 7) {} else {}

1 2 3 4 5 6 7

If(a > 4 && b >= 7)   {}   else   {}

Test Requirements

a > 4	b >= 7	Decision Outcome
True	Don’t care	Don’t care
False	Don’t care	Don’t care
Don’t care	True	Don’t care
Don’t care	False	Don’t care
Don’t care	Don’t care	True
Don’t care	Don’t care	False

Test Cases

How many test cases are required for Condition/Decision Coverage

Total number of test cases = Total conditions * 2 +  Total Decisions * 2

Explanation of formula:

• Condition 1: a > 4  (*2 because it has only two values, True and False)
• Condition 2: b >= 7 (*2 because it has only two values, True and False)
• Decision 1:  If(a > 4 && b >= 7) (*2 because it has only two values, True and False.

Important Points of Condition Decision Coverage (CDC)

1. Condition Decision Coverage (CDC) subsumes Condition Coverage and Decision Coverage. It means that if we performed CDC testing, then no need to perform Condition Coverage and Decision Coverage.
2. CDC is more strong than condition coverage.
3. CDC is more strong than decision coverage.
4. CDC ensures that all conditions and decisions are working fine or not.
5. CDC is weaker than MCDC.
6. CDC is weaker than MCC.