According to Modified Condition Decision Coverage criteria, we need to cover all those combinations of truth values of conditions in which each of the condition’s truth values determines the decision truth value.
What are the conditions in software testing?
Conditions are atomic conditions in expressions.
What are Decisions in software testing?
Decisions are the controls that can control the program flow after evaluating the full expression.
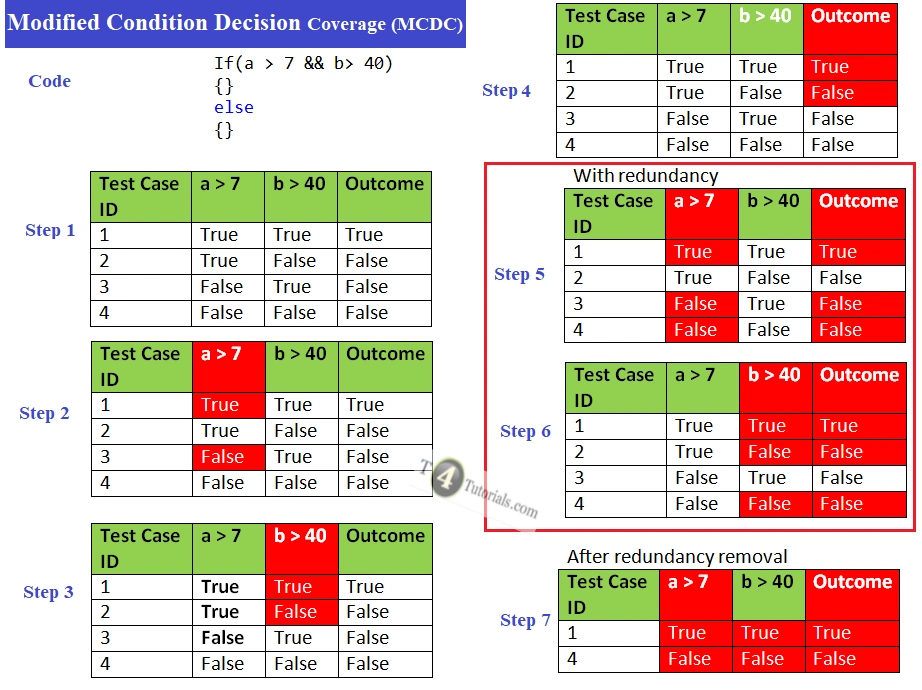
Example 2
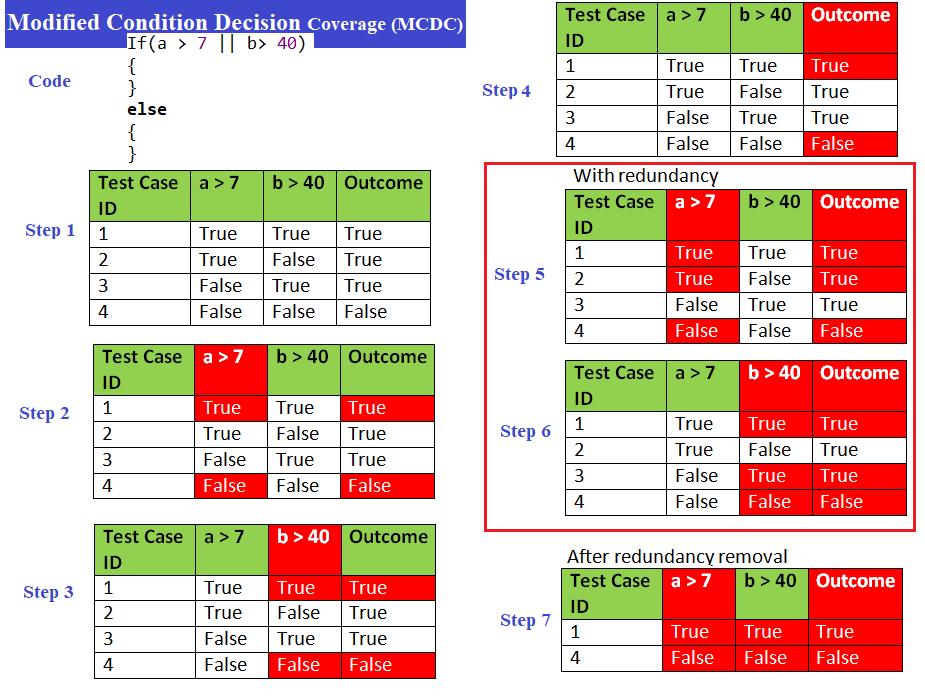
Multiple condition coverage (MCC)
|
1 2 3 4 5 6 7 |
If(a > 7 || b> 40) {} else {} |
Test Requirements for Modified Condition Decision Coverage (MCDC)
Requirement 1: Every condition participating in the decision must have one True and one False value.
Requirement 2: Every decision in a program must have at least one True and one False value.
Requirement 3: Each condition at least one time must independently determine the decision outcome to make it True or False.
| Test Case ID | a > 7 | b > 40 | Outcome |
| 1 | True | True | True |
| 2 | True | False | True |
| 3 | False | True | True |
| 4 | False | False | False |
Fulfilling Requirement 1: Every decision in a program must have at least one True and one False value.
| a > 7 |
| True |
| True |
| False |
| False |
| b > 40 |
| True |
| False |
| True |
| False |
Fulfilling Requirement 2: Every decision in a program must have at least one True and one False value.
| Outcome |
| True |
| True |
| True |
| False |
Requirement 3: Each condition at least one time must independently affect the decision outcome to make it True or False.
| a > 7 | Outcome | |
| 1 | True | True |
| 2 | True | True |
| 3 | False | True |
| 4 | False | False |
| b > 40 | Outcome | |
| 1 | True | True |
| 2 | False | True |
| 3 | True | True |
| 4 | False | False |
Example
For example, if the condition is True then a decision must also be True. Similarly, if the condition is False, then the decision must also be false.
| Condition C1 | Condition C2 | Decision D1 | |
| T | T | T | C1 determines D1 as T |
| F | T | F | C1 determines D1 as F |
Table 1: C1 determines D1.
| Condition C1 | Condition C2 | Decision D1 | |
| T | T | T | C2 determines D1 as T |
| T | F | F | C2 determines D1 as F |
Table 2: C2 determines D1.
| Condition C1 | Condition C2 | Decision D1 | |
| T | T | T | C1 determines D1 as T |
| F | T | F | C1 determines D1 as F |
| T | T | T | C2 determines D1 as T |
| T | F | F | C2 determines D1 as F |
Table 3: C1 and C2 determines D1.
Now, we can remove the redundancy. Redundancy is mentioned below;
| T | T | T | C1 determines D1 as T |
| T | T | T | C2 determines D1 as T |
Both of these two testing the same thing, so we can choose one of them to remove. In this example we have chosen the following;
| T | T | T | C2 determines D1 as T |
| Condition C1 | Condition C2 | Decision D1 | |
| T | T | T | C1 determines D1 as T |
| F | T | F | C1 determines D1 as F |
| T | F | F | C2 determines D1 as F |
Table 4: After removing redundancy.
Now, we can see in table 4 that conditions determine the decision
- If C1 is T then D1 is T
- If C1 is F then D1 is F
- If C2 is T then D1 is T, but it is removed because it is redundant to (if C1 is T then D1 is T).
- If C2 is F then D1 is F
MCC= MCC stands for Multiple condition Coverage.
MCDC= MCDC stands for Modified Condition Decision Coverage.
CDC= CDC stands for Condition Decision Coverage.
CC= CC stands for condition Coverage.
DC= DC stands for Decision Coverage.
Some facts about Modified Condition Decision Coverage (MCDC)
Modified Condition Decision Coverage (MCDC) subsumes CDC. So it leads to the followings;
CDC subsumes CC and DC.
It means that if we performed MCC testing, then no need to perform MCDC, CDC, CC, and DC.
MCDC is stronger than CC.
MCDC is stronger than DC.
MCDC is weaker than MCC.