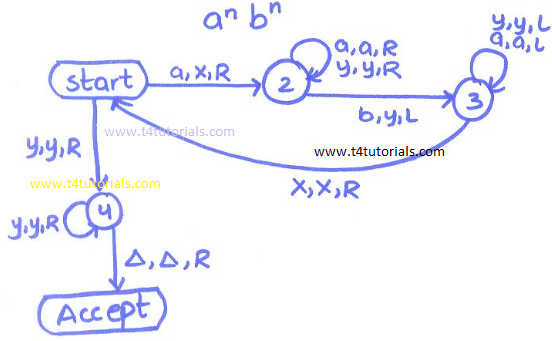
Turing Machine of equal a’s and b’s:

Suppose we want to design a Turing Machine for the language of aⁿbⁿ where a=b.

Logic:

If machine reads anyone a from the input tape, then machine write X and if machine reads any b then machine write y;

a = X

b = Y

Purpose to make every a as X and to every b as Y is only to match one a with one b. This is the way to the bound equal number of a’s and b’s.

Accepted strings:

Such kind of strings should be accepted by Turing Machine.

e.g, ab, aabb, aaabbb,…..etc.

Rejected strings:

Such kind of strings should be rejected by Turing Machine.

e.g, abb, aab, aaabb,…..etc.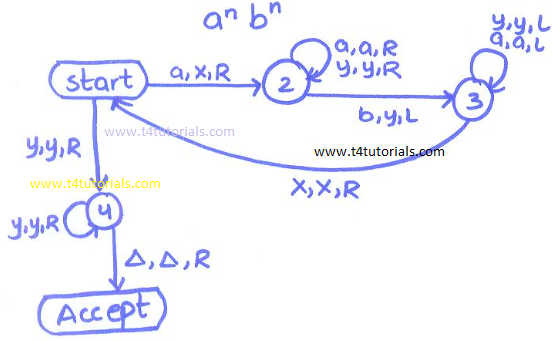

Read More Examples of Turing Machine

1. Turing Machine to copy a string: with animations
2. Turing Machine of numbers divisible by 3: with animations
3. Turing machine for anbncn: with animations

4. Turing machine of two equal binary strings: with animations

5. Turing Machine to Accepts palindromes: with animations

6. Turing machine for a’s followed by b’s then c’s where the number of a’s multiplied by the number of b’s and equals to the number of c’s: with animations

7. Turing machine to Add two binary numbers: with animations

8. Turing machine to  Multiply two unary numbers: with animations
9. Turing machine to Multiply two binary numbers: with animations
10. Turing Machine for the complement of a string
11. Turing Machine for the language of aⁿbⁿ where a=b.
12. Turing Machine for a is less than b, a^mbⁿ where a=b or m=n.

13. Turing machine for the language of all those string in which a is less than b