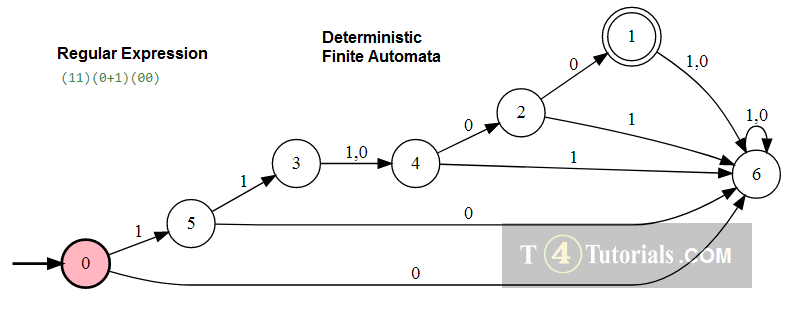
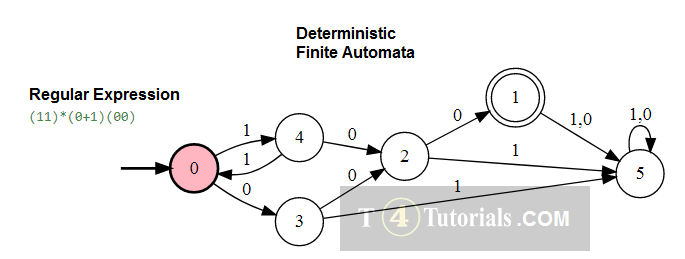
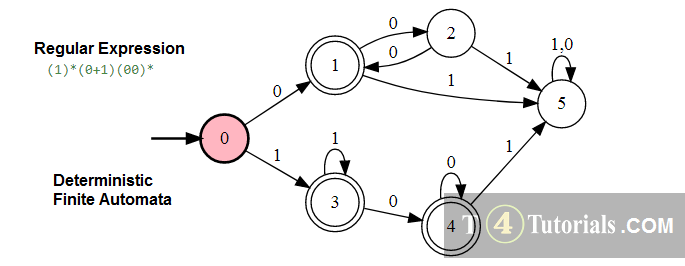
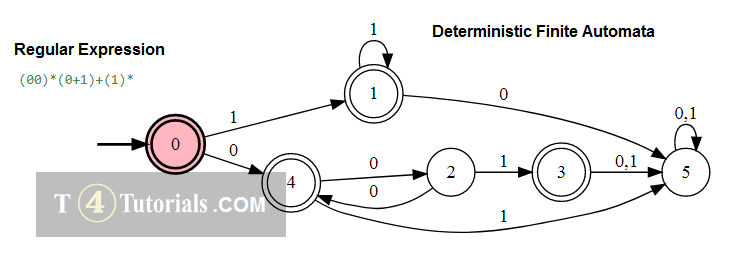
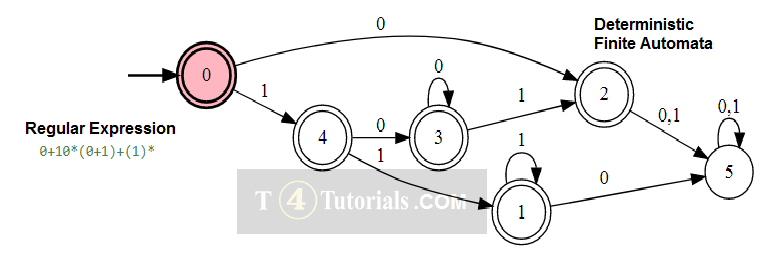
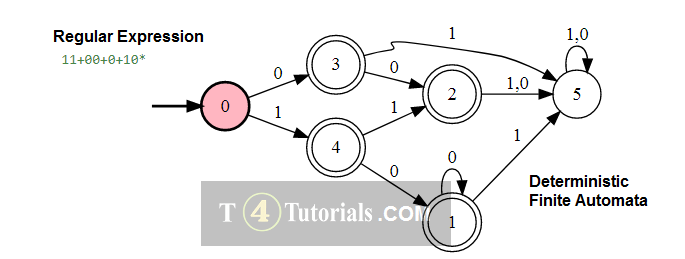
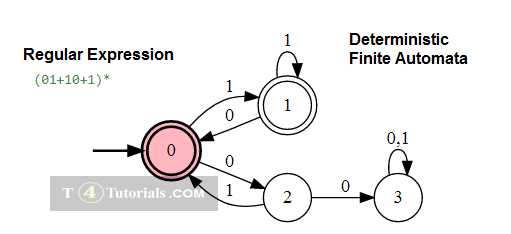
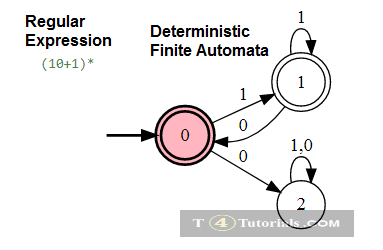
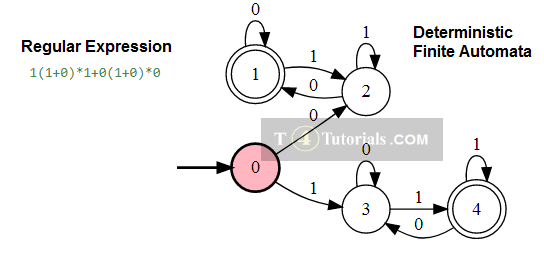
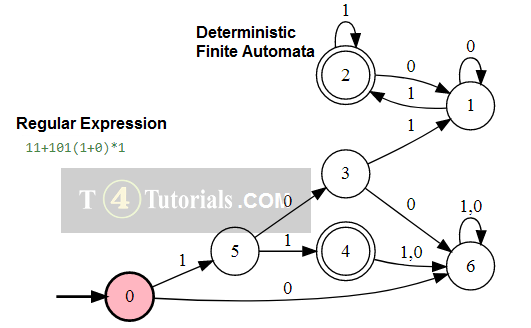
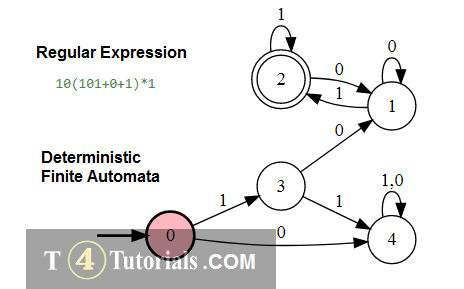
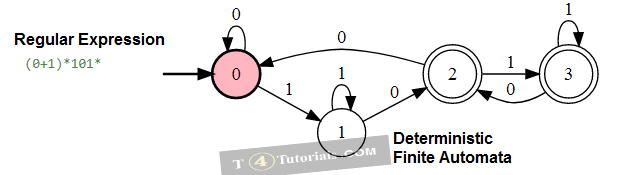
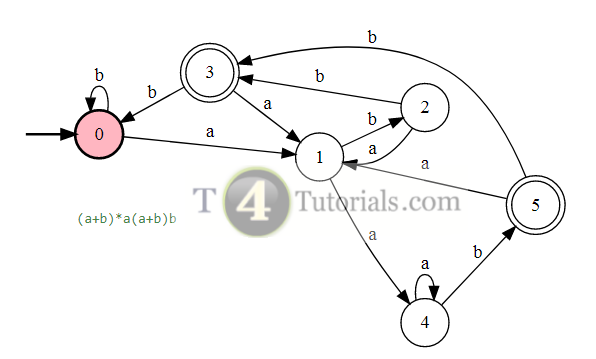
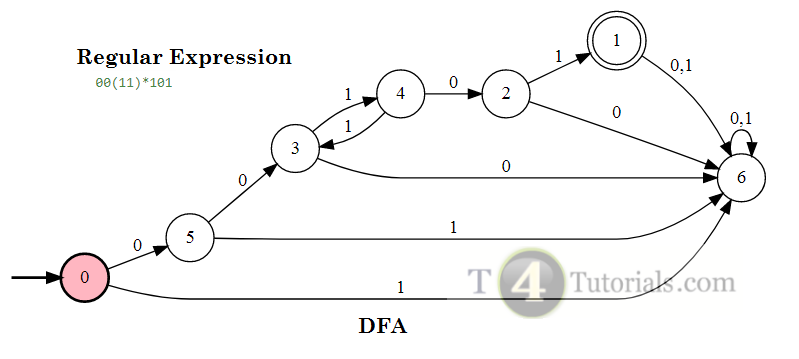
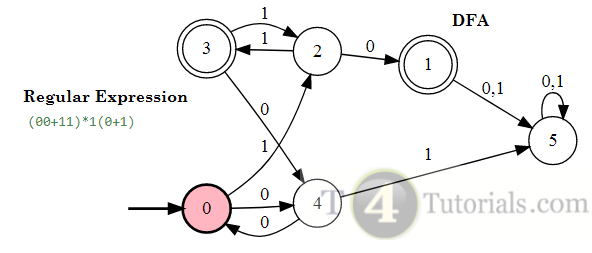
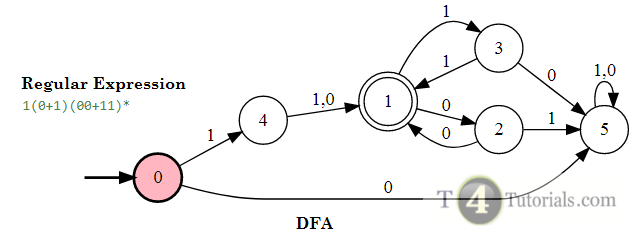
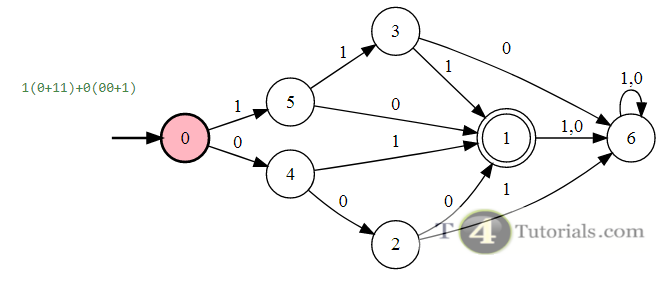
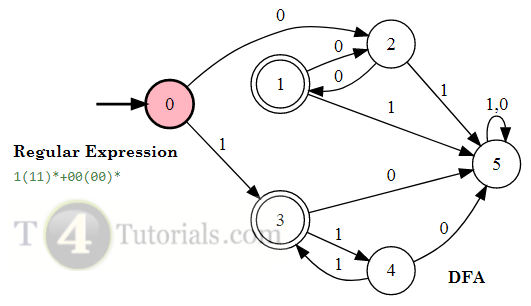
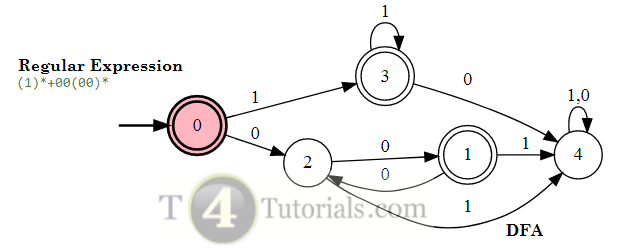
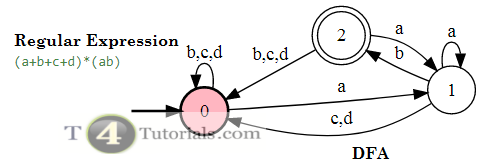
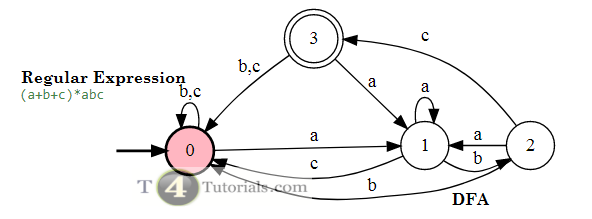
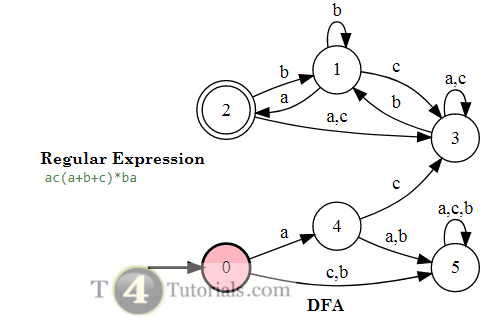
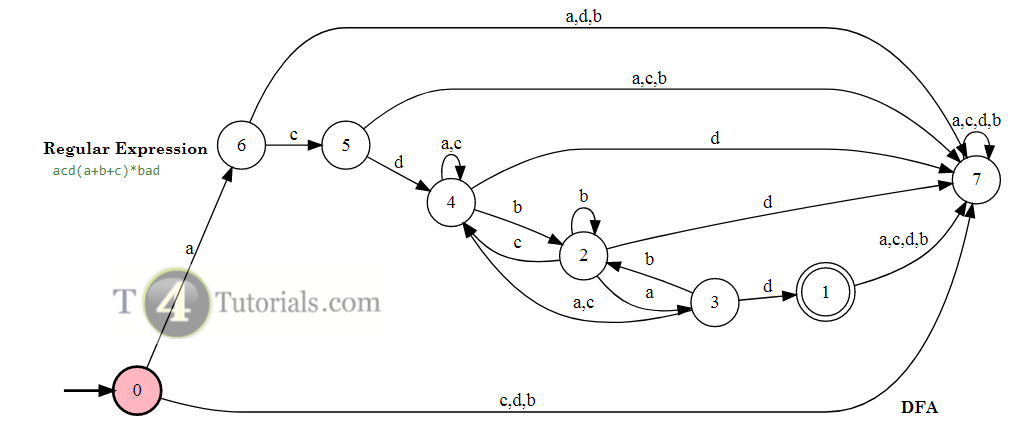
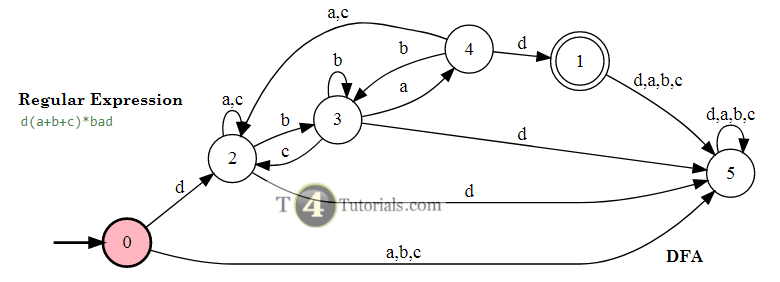
In the Theory of automata, languages can be defined with different techniques. Some of these are mentioned below;
- Language definition by using the Descriptive definition
- Language definition by using the Recursive definition
- Language definition by using the Regular Expressions (RE)
- Language definition by using the Finite Automaton(FA)
\What is Finite State Automata or finite state machine?
The finite state machine is also famous with the following names;
- Finite state automata (FSA)
- Finite automata (FA)
- Finite machines
- Finite state machines
The finite state machine is designed for accepting and rejecting the different strings of the languages from the machine. All regular languages can be represented by the FA.
Symbols of Finite Automata (Finite State Machine FSM)
The finite state machine has the following parts;
Start state: Representing the start of the machine.
Final state: Representing the successful end of the machine
Dead/Dummy State: Having no meaning in the generation of the string. It is only designed to full the requirements of the finite state machines that every state has one transition for each alphabet.
Transition: Representing the reading of the alphabets from the finite state machine.
Strings: Strings are characters or a set of characters that can be accepted or rejected by finite state machines.

Rules of Finite Automata (Finite State Machine FSM)
1. Every state has strictly one transition for each alphabet. Suppose there two alphabets in the languages L={a,b}, then each state has strictly had two transitions. One transition for alphabet a and one transition for alphabet b. Let’s have another example, Suppose there three alphabets in the languages L={a,b,c}, then each state has strictly three transitions. One transition for alphabet a, one transition for alphabet b and one transition for alphabet c.
2. If the generation of any alphabet from a transition is the cause of generating some strings that are not the part of the language, and it becomes very necessary to put that alphabet on some transition, then generates the alphabet and move the machine to the dead/dummy state. Dummy state means that machine will not generate any string.
3. Every string that is part of the language should be accepted by the FSA and every string that is not part of the language should be rejected by the FSA.
4. Every language that can be generated by a regular expression can be generated by FSA.
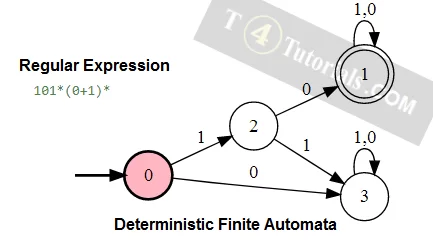
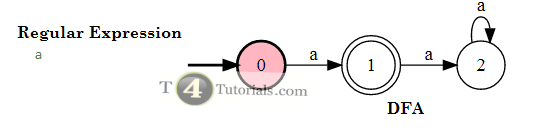
Finite automata for single a
0 is the starting state. 1 is the ending state. 2 is the dummy state.
From state 0 we will start and read a and move to the state a and this is ending state and now we are at ending state. So, it means that the strings is accepted.
Why we generate a transition of a from state 1 to state 2?
Its only to fulfill the rule that every state must have one transition of each alphabet of the langauge. No more transition, no less transition.
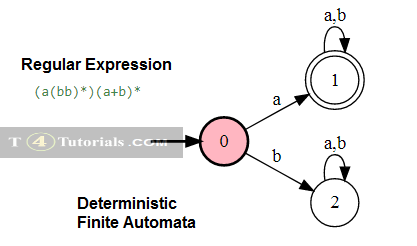
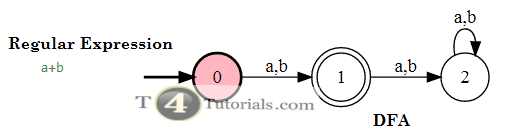
Deterministic Finite automata for a or b
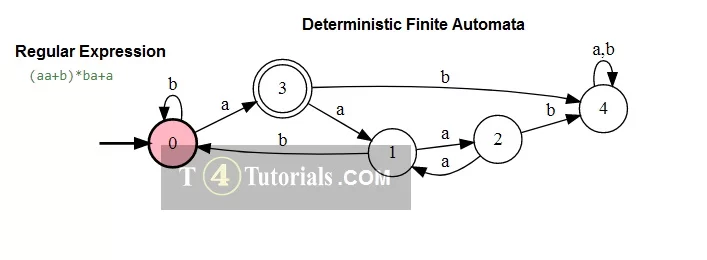
Deterministic Finite automata for a or b whole asterisk (a+b)*

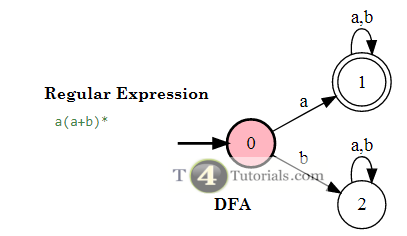
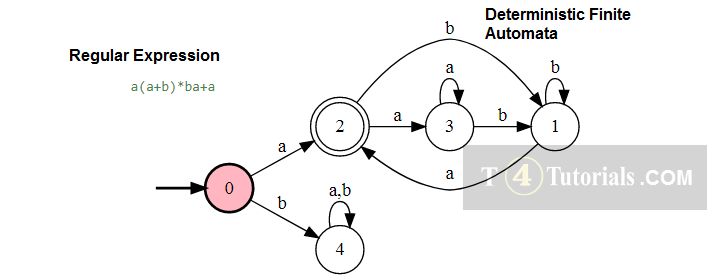
Deterministic Finite automata for a(a+b)*
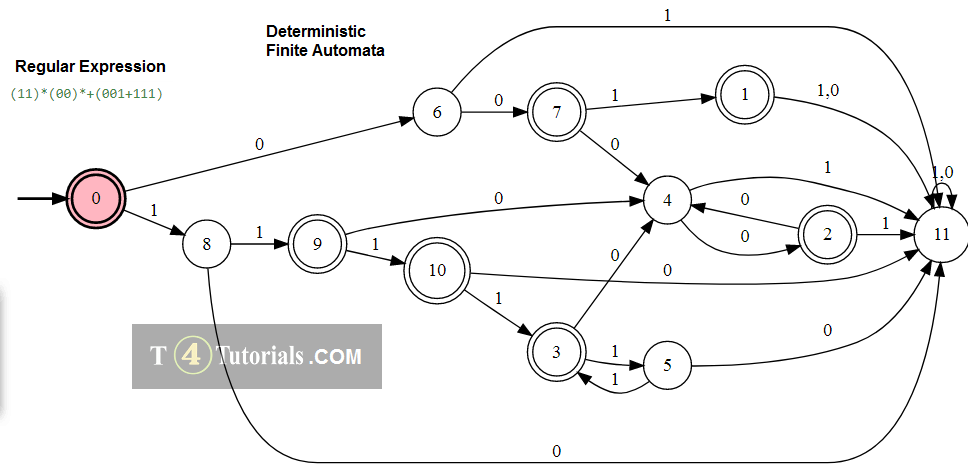
Deterministic finite automata examples and solutions
Example 1
Language of all those strings follows the following rules;
- can’t have odd a’s except single a
- can have many b with even a’s or no a’s.
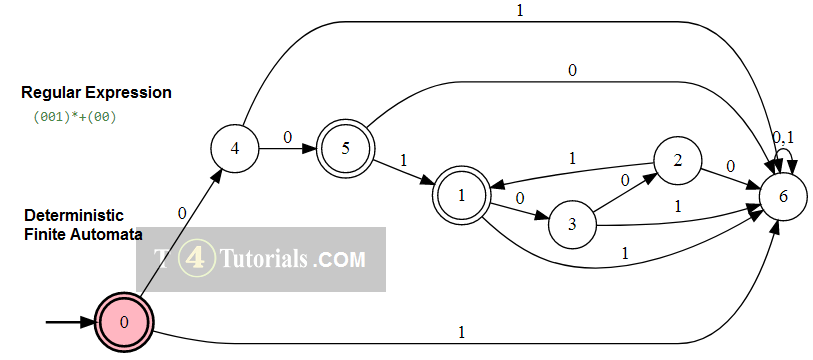
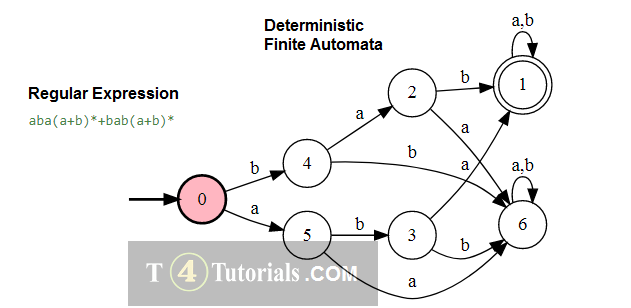
Example 2
Language of all those strings follows the following rules;
- can’t have odd a’s except single a
- can have many b with even a’s or no a’s.
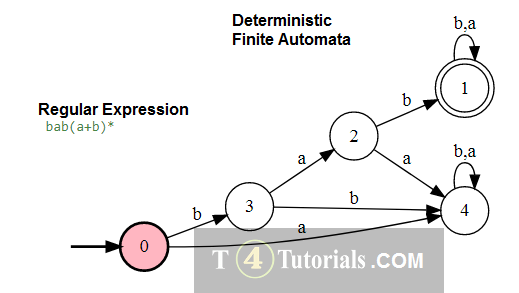
Example 3
Language of all those strings follows the following rules;
- can have many b or many or no aa but all strings must ends with only ba or a.
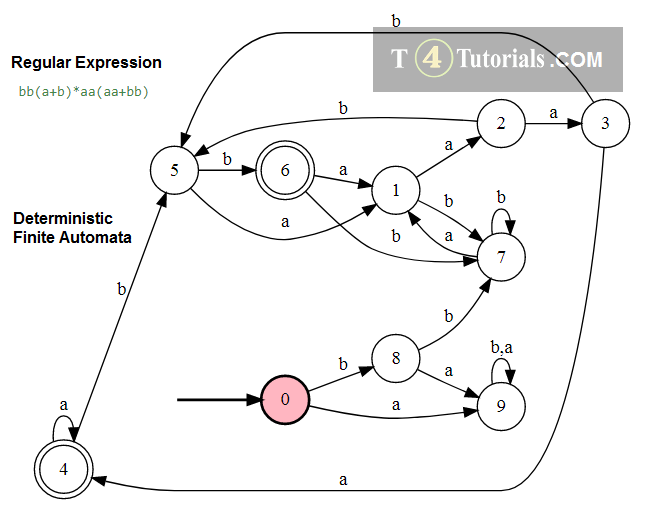
Example 4
Language of all those strings follows the following rules;
- must starts with a and then can have no or many a’s or b’s and ends with only ba or a
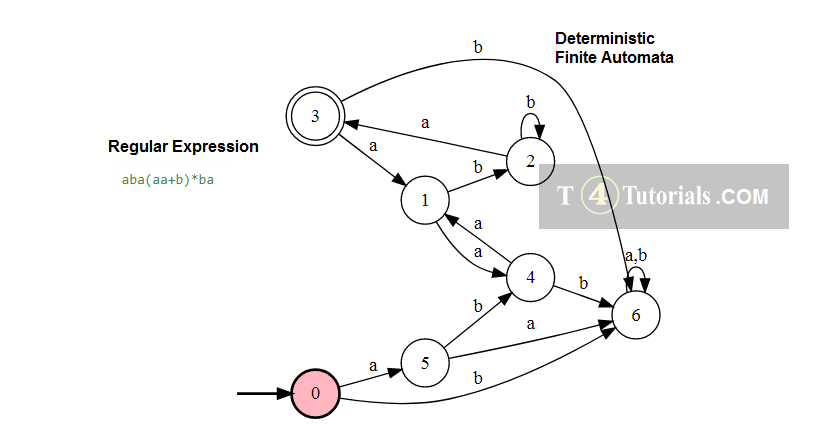
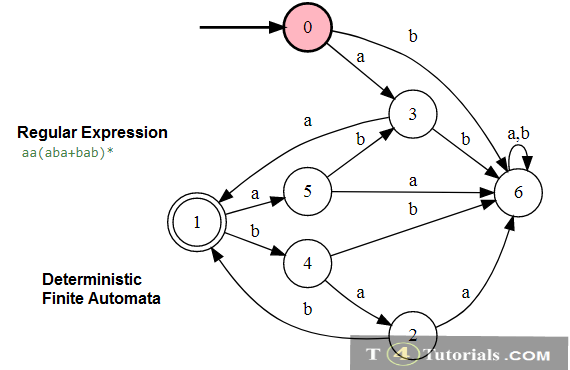
Example 5
Language of all those strings follows the following rules;
- starts with aba and then can have no or many aa and many b and always ends with ba.
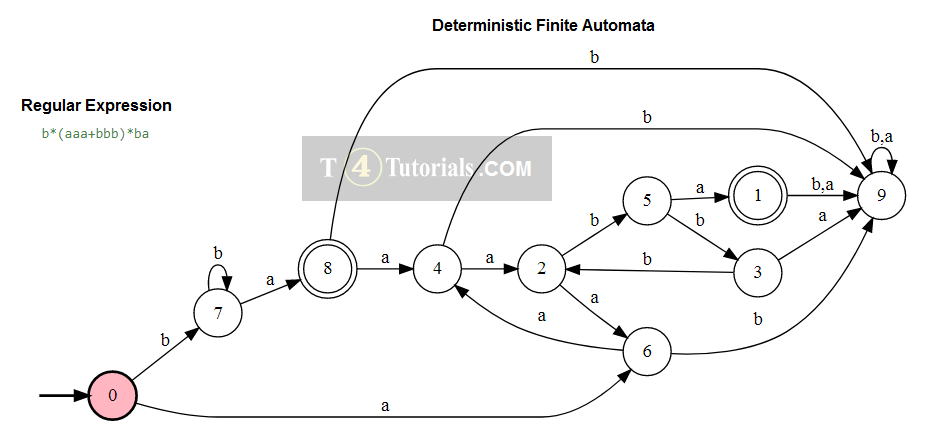
Example 6
Language of all those strings follows the following rules;
- many b’s but only at the begining
- many or no aaa or bbb and then always ends with bs.
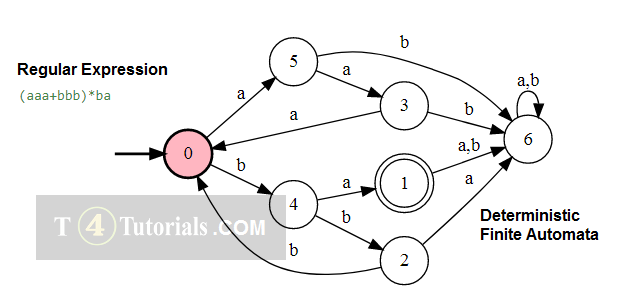
Example 7
Language of all those strings follows the following rules;
- can have no or many aaa’s or bbb’s and always end with ba.
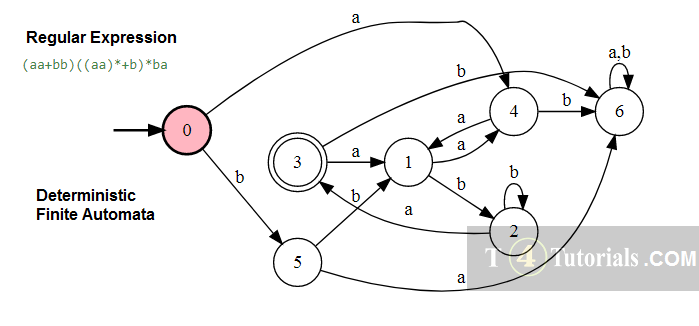
Example 8
Language of all those strings follows the following rules;
- always starts with aa or bb and then can have no or many aa’s or b’s and then always must end with ba.
Example 9
Language of all those strings follows the following rules;
- only two strings are accepted, 11000 or 11100 and no more string.
Example 10
Language of all those strings follows the following rules;
always ends with 000 or 100 and can have no or many 11’s in the starting of the string.
Example 11
Example 12
Example 13
Language of all those strings follows the following rules;
Example 14
Language of all those strings follows the following rules;
Example 15
Language of all those strings follows the following rules;
Example 16
Language of all those strings follows the following rules;
Example 17
Language of all those strings follows the following rules;
Example 18
Language of all those strings follows the following rules;

Example 19
Language of all those strings follows the following rules;
Example 20
Language of all those strings follows the following rules;
Example 21
Language of all those strings follows the following rules;
Example 22
Example 23
Example 24
Example 25
Example 26
Example 27
Example 28
Valid string’s
Examples of some(not all) valid strings are mentioned below;
Length 1= { no strings}
Length 2= {no strings}
Length 3= {aba , bab, no more string}
Length 4= {abaa, abab, baba, babb, no more string}
Invalid strings
Examples of some(not all) invalid strings are mentioned below;
Length 1= { a,b, no more string}
Length 2= {ab, ba, aa, bb, no more string}
Length 3= { aaa, bbb, baa, abb, bba,………and many other similar strings }
Length 4= {aaaa, bbbb, bbaa, aabb,……. and many other similar strings}
Example 29
Example 30
Example 31
Example 32
Example 33
Example 34
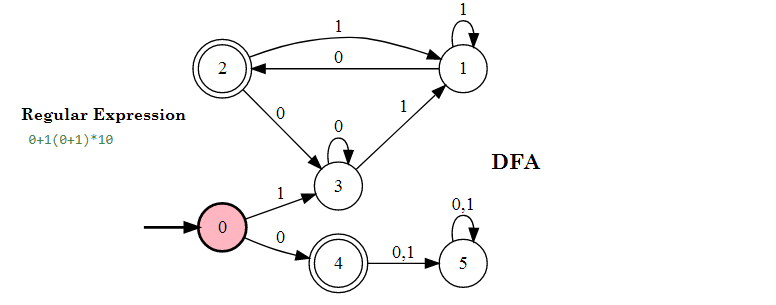
Example 35
Example 36
VALID STRINGS
Examples of some(not all) valid strings are mentioned below;
Strings of length 1={10,11, and no more}
Strings of length4 ={1000,1011,1100,1111, and no more strings}
Strings of length 8={10000000,11000000,11111111,….. and many other similar strings}
INVAID STRING
Examples of some(not all) invalid strings are mentioned below;
Strings of length 2={00, and no more strings}
Strings of length 3={001,100,and more strings}
Strings of length 8={11011111,110100,and more strings}
Example 37
Example 38
Example 39
Example 40
Example 41
Example 42
Valid strings:
Examples of some(not all) valid strings are mentioned below;
Length 1: {No possible valid strings of length 1}
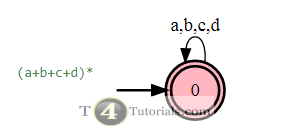
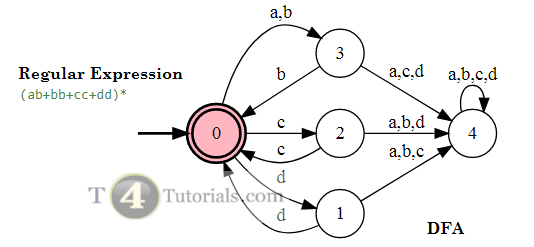
Length 2: {ab, bb, cc, dd and no more possible valid string of length 2}
Length 3: {No possible valid strings of length 3}
Length 4: {abbb, abcc, abdd, bbcc, bbdd, bbab, ccdd, and many more possible strings of length 4}
Invalid strings:
Examples of some(not all) invalid strings are mentioned below;
Length 1: {a, b, c, d, and no possible invalid strings of length 1}
Length 2: {aa, ba, bc, cb,……. and many other similar strings}
Length 3: {aba, abb, acc, abd, add, bcd, dba……. and many other similar strings}
Length 4: {babb, cbba, dcba, ddbc, bbcd……. and many other similar strings}
Example 43
Example 44
Example 45
Example 46
Example 47
Example 48
Example 49
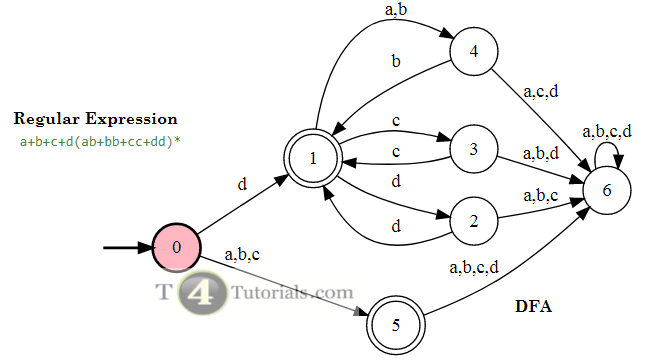
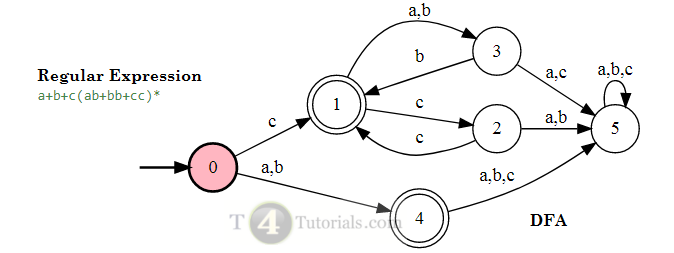
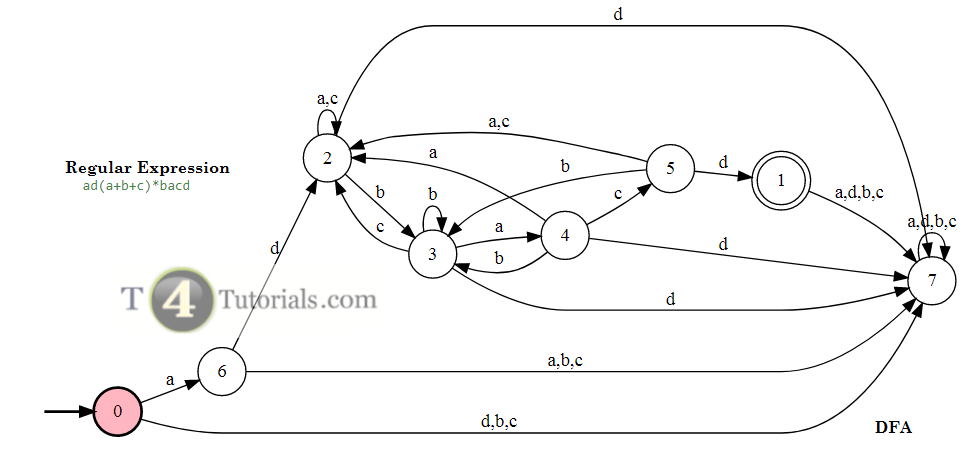
Regular Expression: ad (a + b + c) * bacd
Valid Strings
Examples of some(not all) valid strings are mentioned below;
Valid Strings of Length 1 = No Possible Strings
Valid Strings of Length 2 = No Possible Strings
Valid Strings of Length 3 = No Possible Strings
Valid Strings of Length 4 = No Possible Strings
Invalid Strings
Examples of some(not all) invalid strings are mentioned below;
Invalid Strings of Length 1 = {a, b, c, d, No More Possible Strings}
Invalid Strings of Length 2 = {ad, aa, ac, ad,…. and many other similar strings}
Invalid Strings of Length 3 = {adc, adb, ada,…. and many other similar strings}
Invalid Strings of Length 4 = {adac, abdc, aabac,…. and many other similar strings}
Finite Automata Exercise Solution
Here I am showing you a list of some more important Deterministic Finite Automata used in the theory of automata and theory of computation.
- DFA for (a+b)* (a+b)a .
- DFA for (bb)*(aa)* .
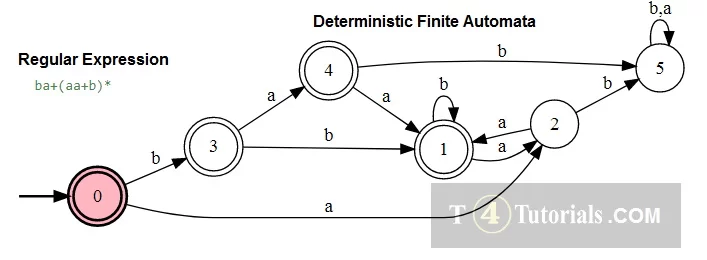
- DFA for b+a(a+b)*+a.
- DFA for (a+b)*b+(bb)*a.
- DFA for bb+a(a+b)*+aa.
- DFA for a(a+b)*+bb(a)* .
- DFA for a(a+b)b*+bb(a)*.
- DFA for b(aa)*a+a(bb)*b.
- DFA for a+a(aa+b)*(aa)b.
- DFA for a+a(aa+b)*+(aa)b.
- DFA for (a+b)b(a+b)*+(aa)*b.
- FA for strings starting with a and ending with a.
- FA for the language of all those strings starting with a.
- FA for the language of all those strings containing aa as a substring.
- DFA for the language of all those strings starting and ending with the same letters.
- DFA for the language of all those strings starting and ending with different letters.
- DFA for the language of all those strings having double 0 or double 1.
- DFA for the language of all those strings starting and ending with b.
- DFA for ending with b.
- DFA for the string of even A’s and even b’s.
- DFA for the regular expression of a(a+b)*+(bb)+a(ba)*+aba+bb*(a+b)*.
- RegExp and DFA for strings having triple a’s or triple b’s.
- Finite Automata of all strings divisible by 4
- Finite automata for all strings with at least one a
- Finite automata for all strings with at least two a
- Finite automata for all strings with exactly two b
- Finite automata for at least one a and at least one b
- Finite automata for strings end in a double letter (two a’s or two b’s)
- Finite Automata for All strings containing exactly one a
- 50 Examples of Finite automat