Turing machine for the language of all those string in which a is less than b, ambn, where a<b
Explanation of diagram:
Start:
Start of machine operation
From start, there is a,x,r
Read a, write X, move right
From state 2, read a, write a and move right or read Y, write Y, move right.
From state 2, Read B, Write Y, write Y and move right.
Halt state:
Halt state is the ending state.
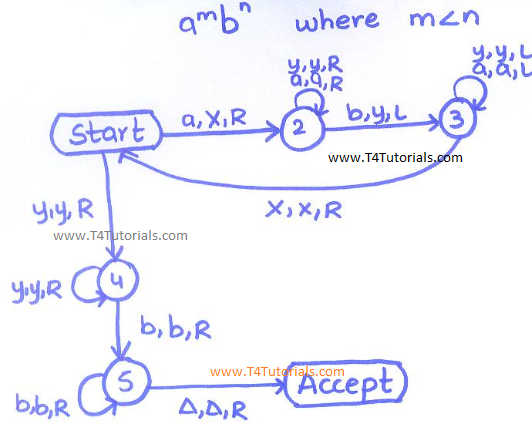
Figure: Turing machine for a is less than b

Read More Examples of Turing Machine
- Turing Machine to copy a string: with animations
- Turing Machine of numbers divisible by 3: with animations
- Turing machine for anbncn: with animations
-
Turing machine of two equal binary strings: with animations
-
Turing Machine to Accepts palindromes: with animations
-
Turing machine for a’s followed by b’s then c’s where the number of a’s multiplied by the number of b’s and equals to the number of c’s: with animations
-
Turing machine to Add two binary numbers: with animations
- Turing machine to Multiply two unary numbers: with animations
- Turing machine to Multiply two binary numbers: with animations
- Turing Machine for the complement of a string
- Turing Machine for the language of anbn where a=b.
- Turing Machine for a is less than b, ambn where a=b or m=n.
-
Turing machine for the language of all those string in which a is less than b