Context Free Grammar CFG in theory of automata

What is Context-Free Grammar CFG?

CFG is a set of rules for automating the machine and generating the strings of a language. CFG generates a pattern of strings.

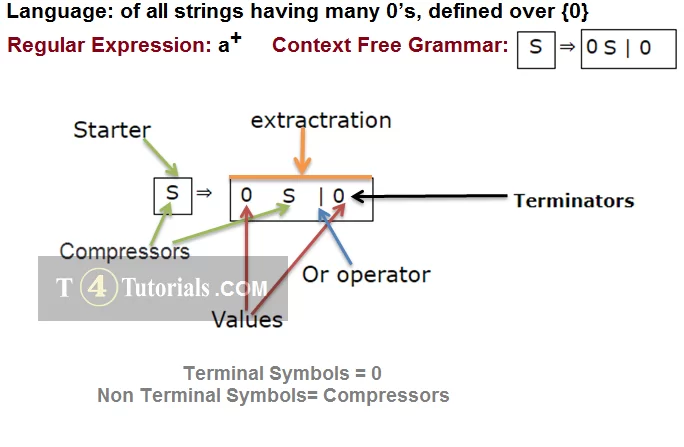
CFG has the following parts;

1. Start symbol
2. Set of terminal symbols
3. Set of non-terminal symbols
4. Set of rules

In easy words, CFG has the following parts;

1. Starters
2. Extraction
3. Compressors
4. Values
5. Operators
6. Terminators

Starters: Starter is the initial compressed variable. CFG have one starting point. Starters are always on left side of the CFG.

Extraction: The extract form of a compressor. The extraction can have alphabets, starters, compressors, values, operators, and terminator etc.It is represented on right side of the CFG.

Compressors: We can extract the Compressor if extraction is required.It is represented on the left side of the CFG.

Values: Value is a string or set of values combine to make a string.

Or operator: Or operator | is used to represent the or operation. For example 0 | 1 can be read as 0 or 1.

Terminators: The ending point of the CFG. More than one options of ending a CFG are possible but while reading a string CFG must end with a one terminator.

Example

Language: of all strings having many 0’s, defined over {0}

Regular Expression: a⁺

Context Free Grammar: S ⇒ 0S | 0

Example 

Language: of all strings having many 0’s or no zero, defined over {0}

Regular Expression: a^*

Context Free Grammar: S ⇒ 0S | ε

Detailed tutorial on what is meaning of null or epsilon

Example 

Language: of all strings having exactly one 0’s or exactly one 1, defined over {0,1}

Regular Expression: 0+1

Context Free Grammar: S ⇒ 0 | 1

Example 

Language: of all strings having many 0’s or many 1’s or no zero or no one, defined over {0,1}

Regular Expression: (0+1)*

Context Free Grammar: S ⇒ 0S | 1S | ε

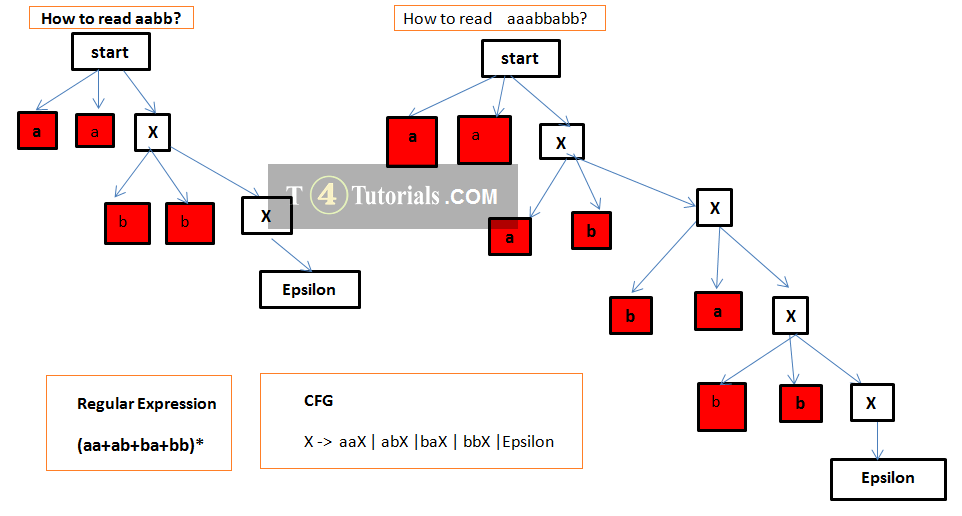
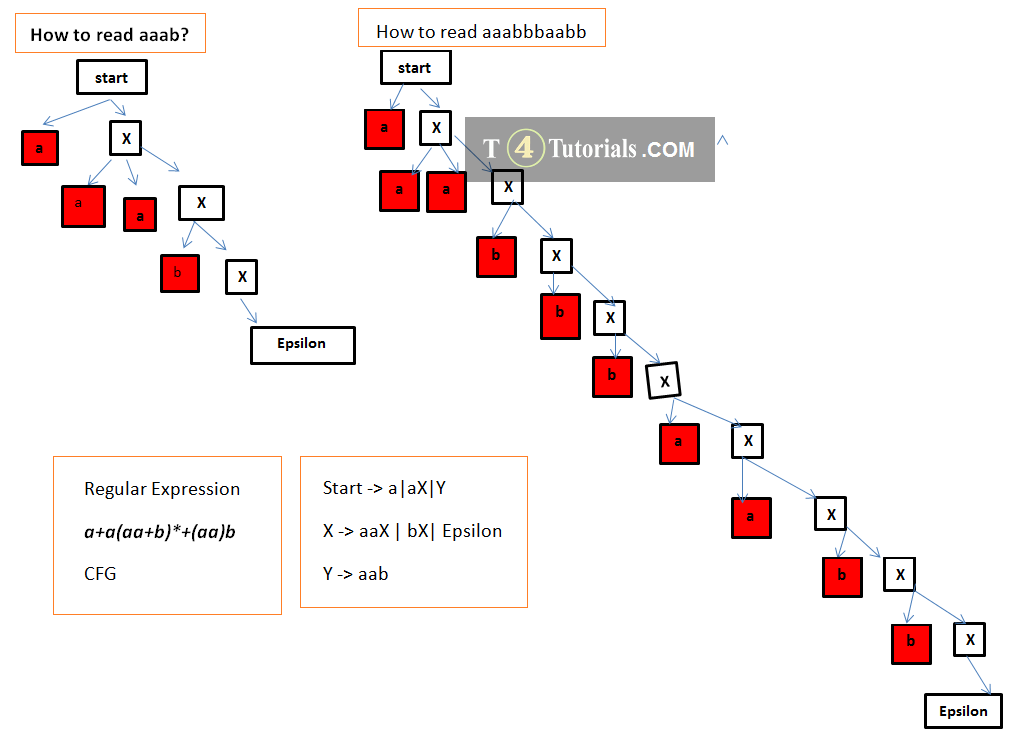
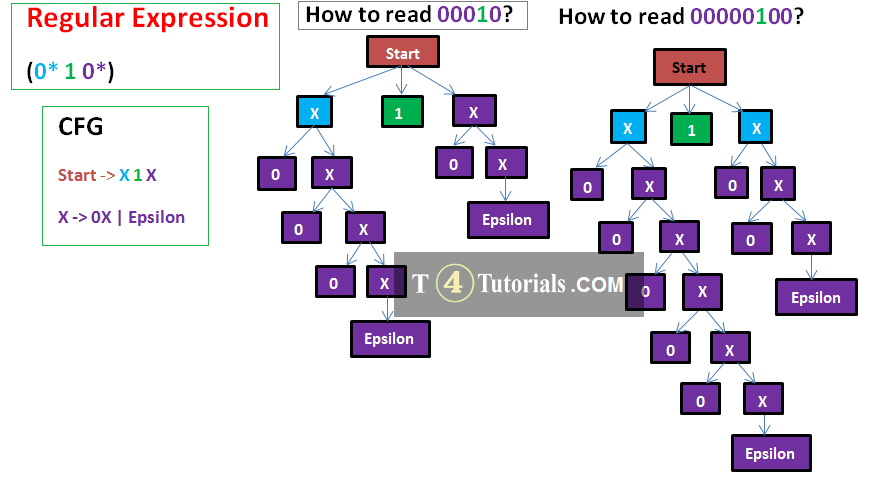
Examples of CFG

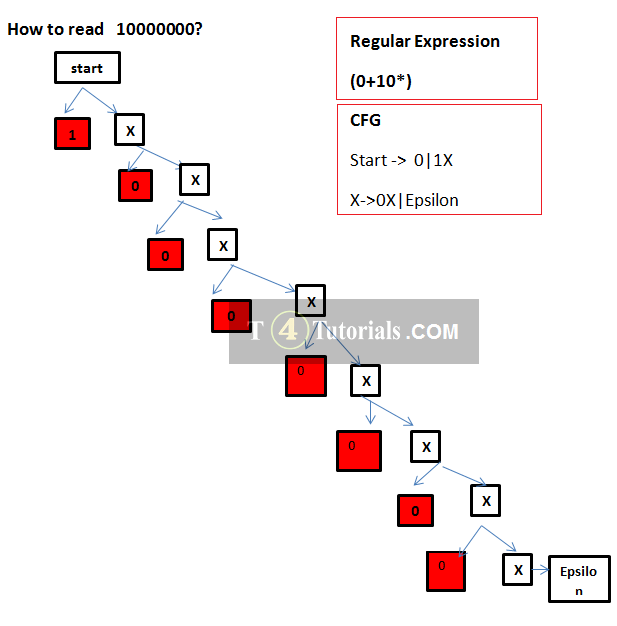
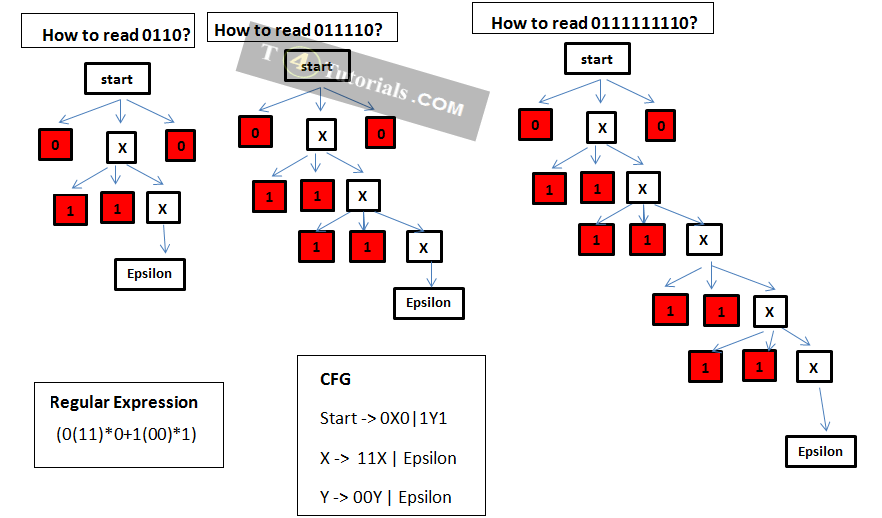
Example 1

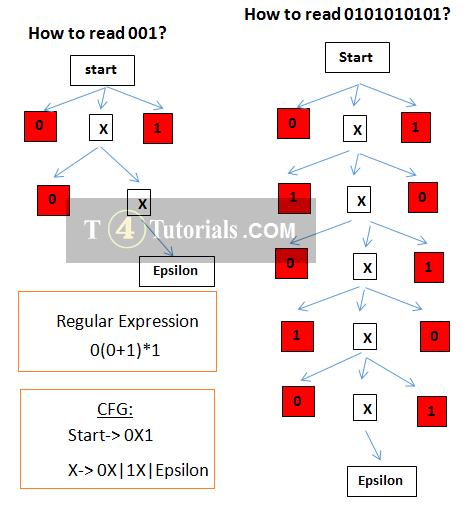
• Starters : start
• Extraction: X1X, 0X, Epsilon
• Compressors: start, X
• Values: 1, 0, Epsilon
• Terminators: Epsilon

Example 2

• Starters : start
• Extraction: 0,1X, 0X,Eosilon
• Compressors: start, X
• Values: 1, 0, Epsilon
• Terminators: 0, Epsilon

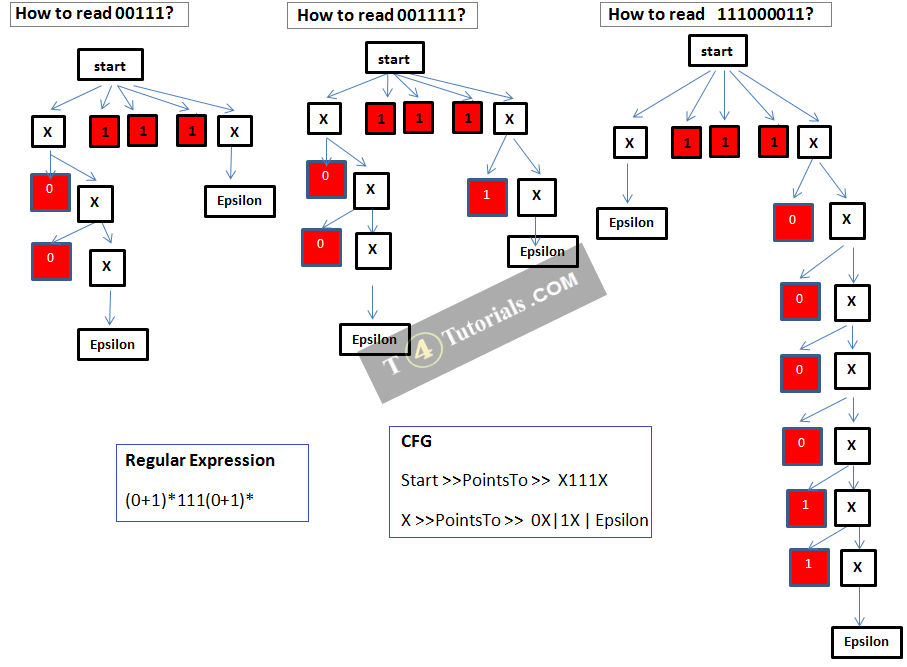
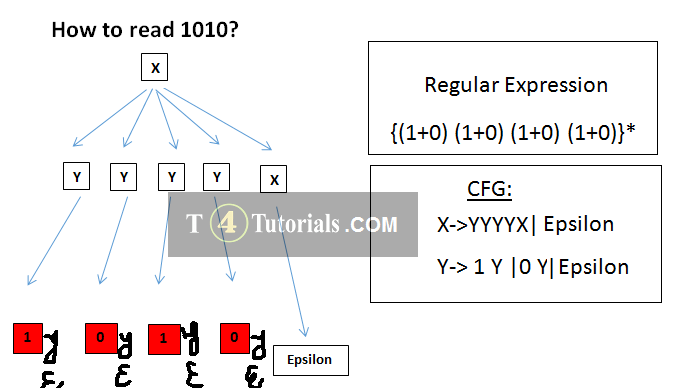
Example 3

• Starters : start
• Extraction: x111X, 0X,1X,Eosilon
• Compressors: start, X
• Values: 1, 0, Epsilon
• Terminators: Epsilon

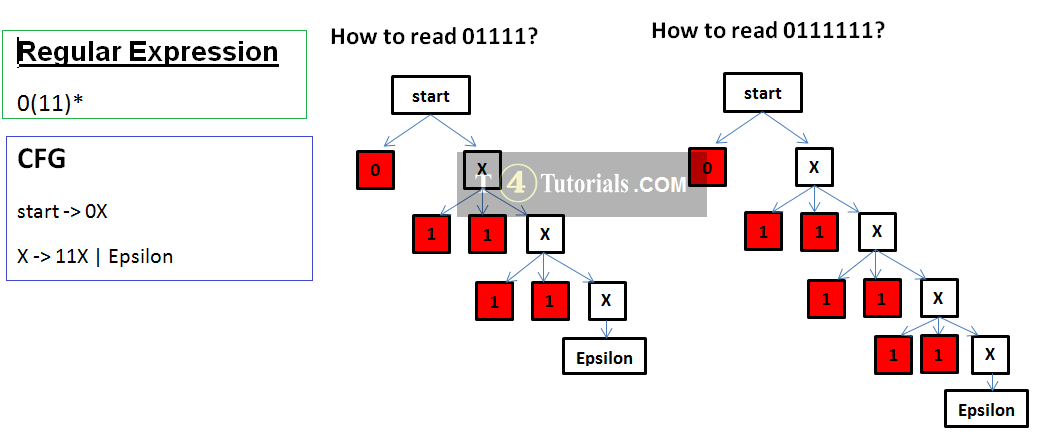
Example 4

• Starters : start
• Extraction: 0X, 11X, Eosilon
• Compressors: start, X
• Values: 11, 0, Epsilon
• Terminators: Epsilon

Example 5

Example 6

Example 7

Example 8

Example 9

Example 10

Example 11

Example 12

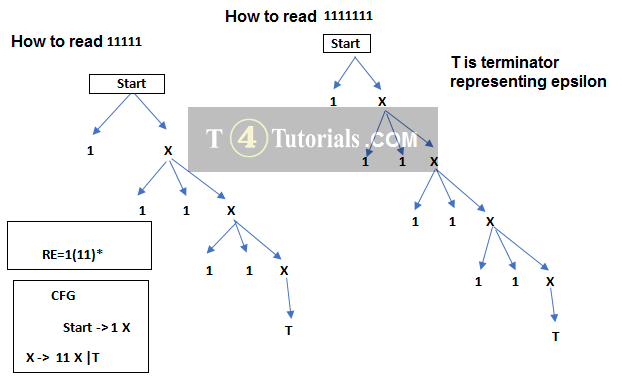
Built the CFG for the language of all those strings having 0 a’s or many a’s?

S ⇒ aS | ε

Now we can read multiple a’s from this CFG.

For example;

To read o a’s from S ⇒ aS | ε

S ⇒ aS | ε

S⇒ ε

To read 1 a from S ⇒ aS | ε

S ⇒ aS

S⇒ a ε

S⇒ a 

To read 2 a from S ⇒ aS | ε

S ⇒ aS

S ⇒ aaS

S⇒ a ε

S⇒ a 

and similarly, we can read many a’s from this CFG.

More Examples of CFG

1. Intro to Context Free Grammar with 12 Examples
2. CFG of Language of all even and odd length palindromes
3. Context Free Grammar CFG for language of all even length strings
4. CFG for the language of all non Palindromes
5. CFG for strings with unequal numbers of a and b
6. CFG of odd Length strings {w | the length of w is odd}
7. CFG of Language contains at least three 1’s or three a’s {w | w contains at least three 1’s}
8. CFG for the language L = 0ⁿ1ⁿ where n>=1
9. CFG for the language L = 0ⁿ1²ⁿ where n>=1
10. Write a CFG for the language L = 0ⁿ1⁴ⁿ where n>=1
11. CFG for {aⁿ b aⁿ⁺¹ | n >=0}
12. CFG for {aⁿ b aⁿ⁺² | n >=0}
13. CFG for {aⁿ b aⁿ⁺³ | n >=0}