Turing Machine to Checks that a binary number is divisible by 3 or not?

A number is divisible by 3 if the sum of its all digits is a multiple of 3 or divisibility by 3.

Multiple of 3:  Any number that three divides evenly or any number for which 3 is a factor. For a number to be divided “evenly” by three the answer must be a whole number with no remainders. So, 30 is a multiple of 3 since 30 / 3 = 10 (10 is a whole number), but 31 is not because 31 / 3 = 10.33

The divisibility rule for 3 states that a number is completely divisible by 3 if the sum of its digits is divisible by 3.

Consider a number, 204. To check whether 204 is divisible by 3 or not, take sum of the digits (i.e. 2+0+4= 6). Now check whether the sum is divisible by 3 or not. If the sum is a multiple of 3, then the original number is also divisible by 3. Here, since 6 is divisible by 3, So 204 is also divisible by 3.

 

Just for practice

Similarly, if you can test that 204 is divisible for other numbers or not.

divisible by 2
Yes
divisible by 3
Yes
divisible by 4
Yes
divisible by 5
No
divisible by 6
Yes
divisible by 7
No
divisible by 8
No
divisible by 9
No
divisible by 10
No
divisible by 11
No
divisible by 12
Yes
divisible by 13
No

Turing Machine divisible by 3Note:

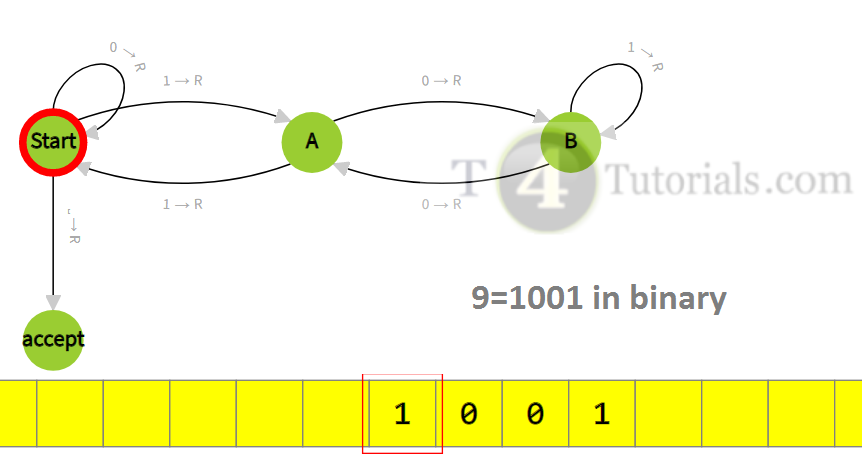
• 1->1->R and 1->R are same things. Both represent read 1, write 1, and move right.
• [ and Delta and empty cell of tape are the same things

Turing machine that checks if the input length is divisible by 3.

Turing Machine divisible by 3 with animations

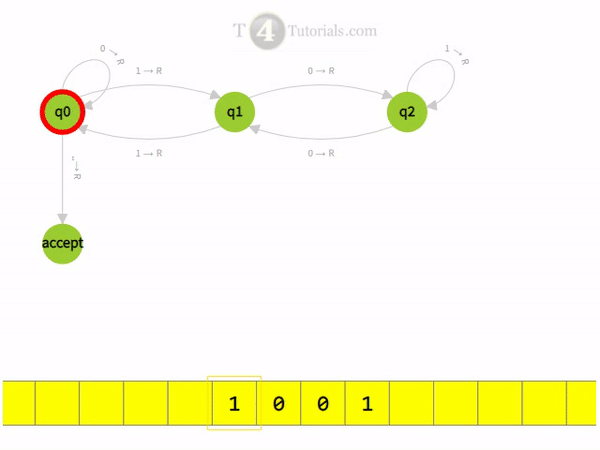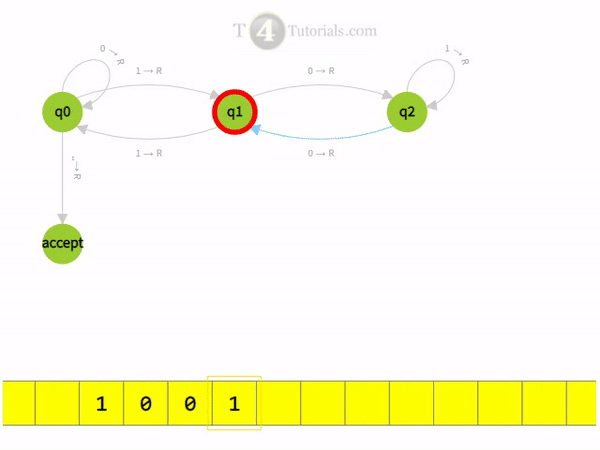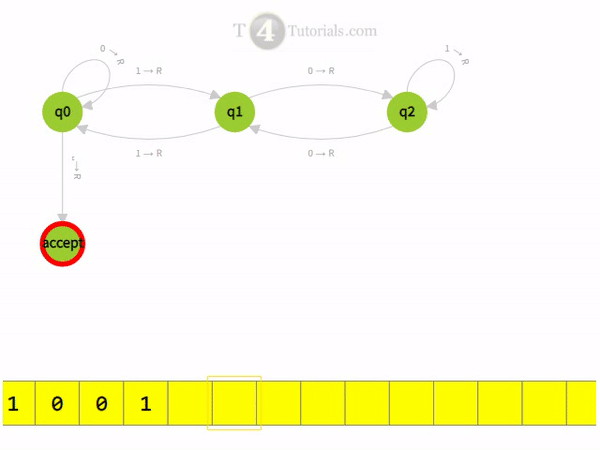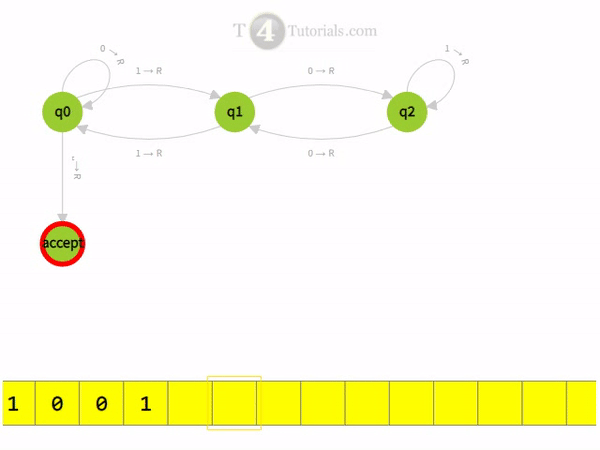
Read More Examples of Turing Machine

1. Turing Machine to copy a string: with animations
2. Turing Machine of numbers divisible by 3: with animations
3. Turing machine for anbncn: with animations

4. Turing machine of two equal binary strings: with animations

5. Turing Machine to Accepts palindromes: with animations

6. Turing machine for a’s followed by b’s then c’s where the number of a’s multiplied by the number of b’s and equals to the number of c’s: with animations

7. Turing machine to Add two binary numbers: with animations

8. Turing machine to  Multiply two unary numbers: with animations
9. Turing machine to Multiply two binary numbers: with animations
10. Turing Machine for the complement of a string
11. Turing Machine for the language of aⁿbⁿ where a=b.
12. Turing Machine for a is less than b, a^mbⁿ where a=b or m=n.

13. Turing machine for the language of all those string in which a is less than b