This tutorial covers the basic concepts of Push Down Automata – PDA.
Representation of PDA
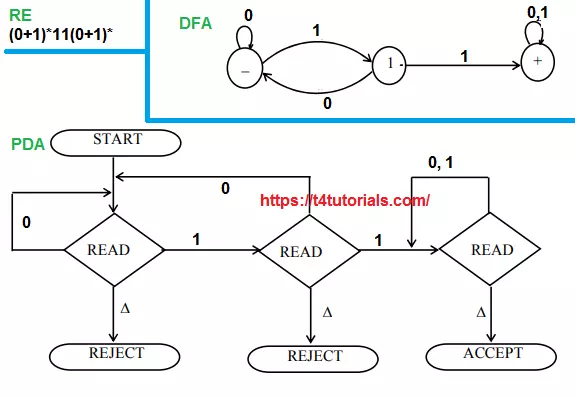
We can represent the PDA with the following two methods;
- Without stack
- No need to use the Stack for Regular languages that can be represented by regular expressions (RE) and Deterministic Finite Automata (DFA);
- With Tape and Stack
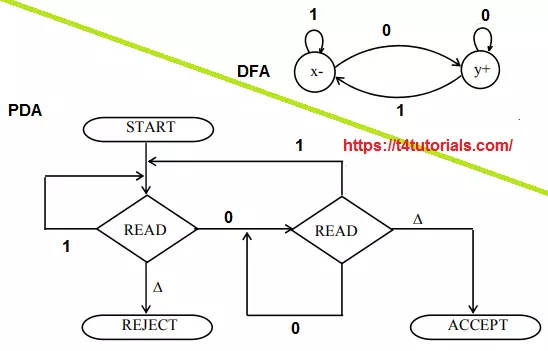
- Some times we need to use the Stack with tape. For example, when the languages can’t be represented with a regular expression or finite automata. If I ask you to draw the finite automata for the language of all those string having a’s just on the left side and b’s on right side of the string, and the length of a’s and b’s must be same. In this case, we cant draw deterministic finite automata but we can write CFG and can draw the PDA for such a problem.
What is Tape?
The tape is the data structure to temporarily store the alphabets of the string.
The Starting state
The START state is the initial state and can be represented by;
Note: Starting state has no alphabet on its arrow.
The Accepting state
The Accept state is the final state representing the successful end of the machine and can be represented by;
A Rejecting state
The reject state is representing the dead or dummy state. When we read an alphabet that is leading to the invalid string for a language, then we draw a transition to the reject state.
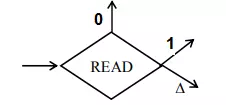
A Reading state
The Read state is to read an input letter and lead it to another state or the same state. The READ state is expressed by;
What is a Stack?
STACK is a memory where the input letters can be placed until it fulfills the logic of the given language to read a string.
PUSH
A PUSH operator adds a new letter at the bottom position of the STACK. For example, if the letters X, Y, and Z are pushed to the STACK that was initially blank, the STACK can be shown as below;
| DELTA |
| X |
| DELTA |
| Y |
| X |
| DELTA |
| Z |
| Y |
| X |
| DELTA |
Note: Stack can have unlimited Delta at the bottom.
POP
A POP operator removes a letter from the top position of the STACK. For example, if the letters X, Y, and Z are pushed to the STACK that was initially blank, the STACK can be shown as below;
| Z |
| Y |
| X |
| DELTA |
| Y |
| X |
| DELTA |
| X |
| DELTA |
| DELTA |
STACK that was initially blank, the STACK can be shown as

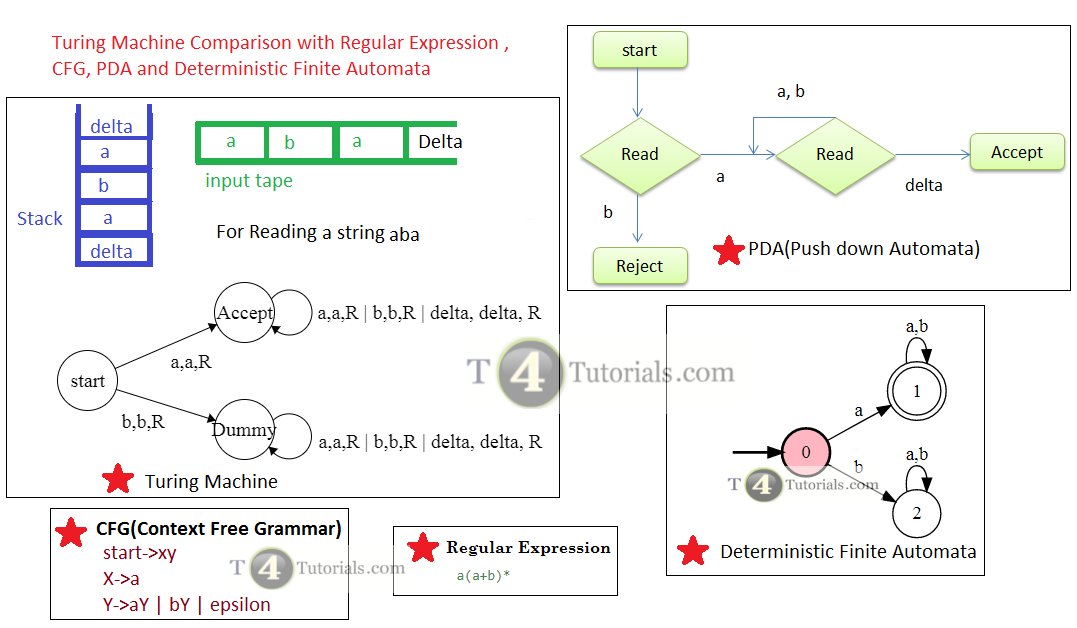
Examples of PDA
- PDA for the language of anbnc2n.
- Push Down Automata For Four Variables, ambncndm.
- Push Down Automata PDA For B Twice. anb2n
- PDA for ambnanbm
- PDA for equal a’s and b’s
- PDA for unequal a’s and b’s