Turing machine for a’s followed by b’s then c’s

Turing machine that Decides the language of

• { a^(i)b^(j)c^(k) | i*j = k and i,j,k ≥ 1 }.
• a’s followed by b’s then c’s,
• where the number of a’s multiplied by the number of b’s and equals to the number of c’s.
  For example:

Valid strings: abc, abbcc, aabbcccc, aabbbcccccc,….

InValid strings: abCc, aabbcc, aaabbcccc, aaabbbbcccccc,…

Let’s test the turning machine with the input as  aabbbcccccc.

Note:

1->1->R and 1->R are same things. Both represent read 1, write 1, and move right.
[ and Delta and empty cell of tape are the same things

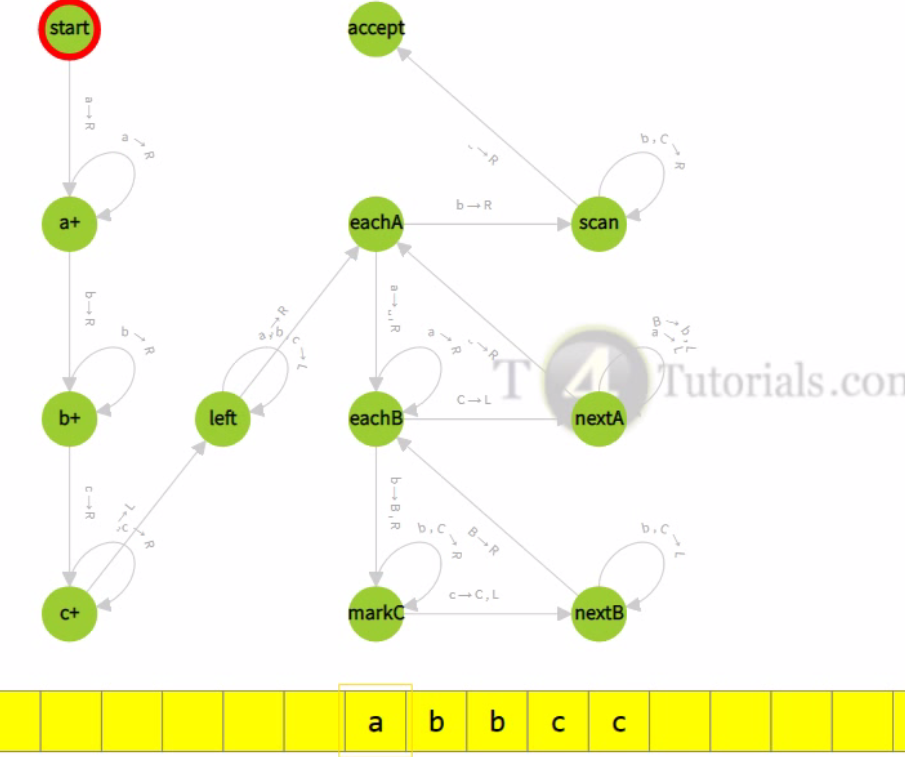
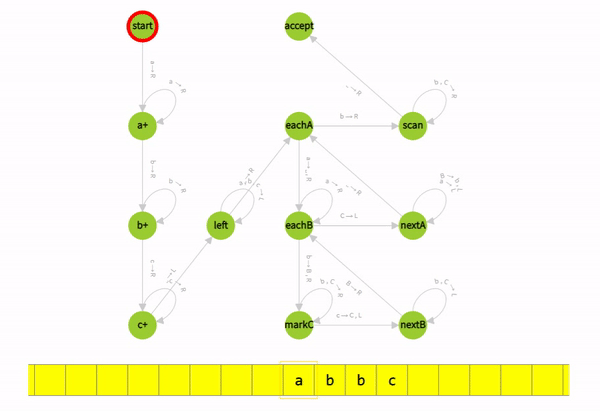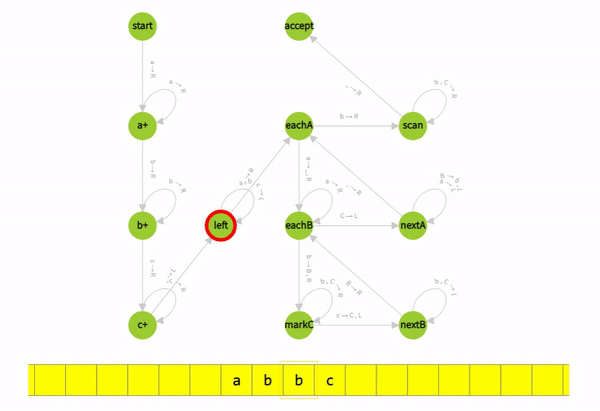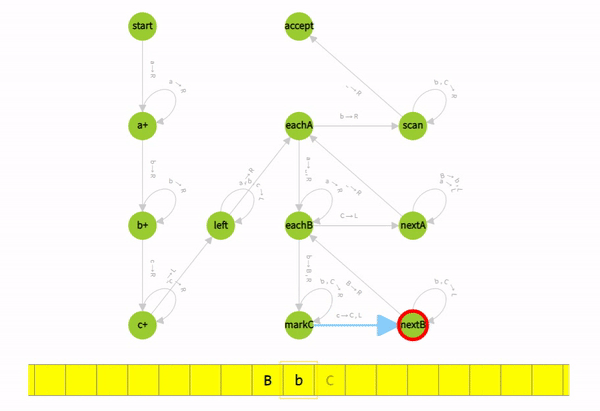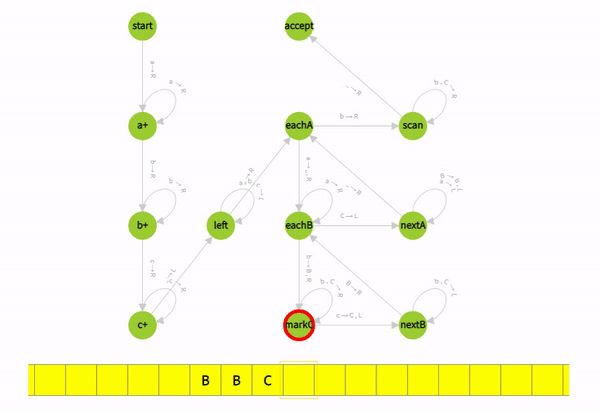
How Turing machine accepts valid strings? with animations

How Turing machine for a’s followed by b’s then c’s accept valid strings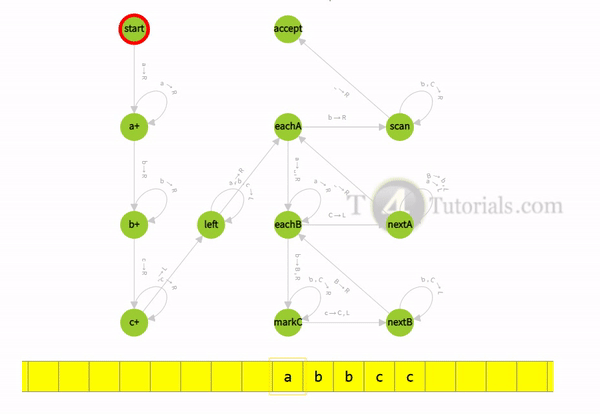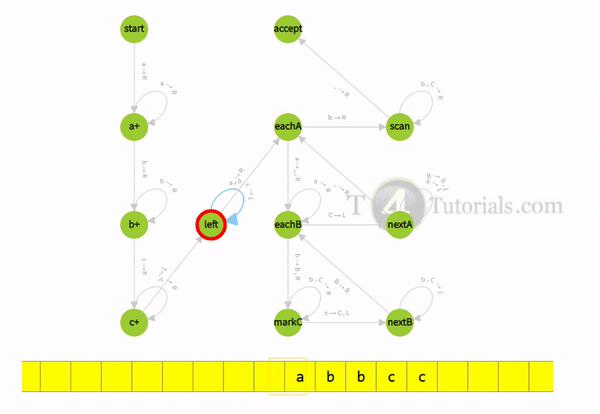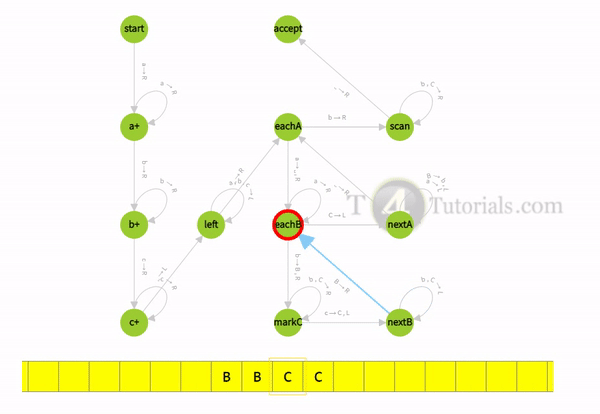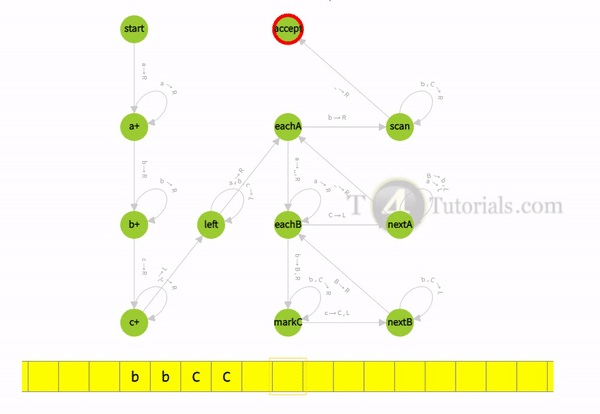

How Turing machine rejects valid strings?

Read More Examples of Turing Machine

1. Turing Machine to copy a string: with animations
2. Turing Machine of numbers divisible by 3: with animations
3. Turing machine for anbncn: with animations

4. Turing machine of two equal binary strings: with animations

5. Turing Machine to Accepts palindromes: with animations

6. Turing machine for a’s followed by b’s then c’s where the number of a’s multiplied by the number of b’s and equals to the number of c’s: with animations

7. Turing machine to Add two binary numbers: with animations

8. Turing machine to  Multiply two unary numbers: with animations
9. Turing machine to Multiply two binary numbers: with animations
10. Turing Machine for the complement of a string
11. Turing Machine for the language of aⁿbⁿ where a=b.
12. Turing Machine for a is less than b, a^mbⁿ where a=b or m=n.

13. Turing machine for the language of all those string in which a is less than b