Turing Machine Basics:
The Turing machine is an invention of a mathematician Alan Turing. Turing machine is a very powerful machine. Any computer problem can be solved through Turing Machine. Just like FA, Turing machine also has some states and some transition. Starting and ending states are also the part of Turing Machine. Every transition on the states have 3 parts;- Read
- Write
- Move
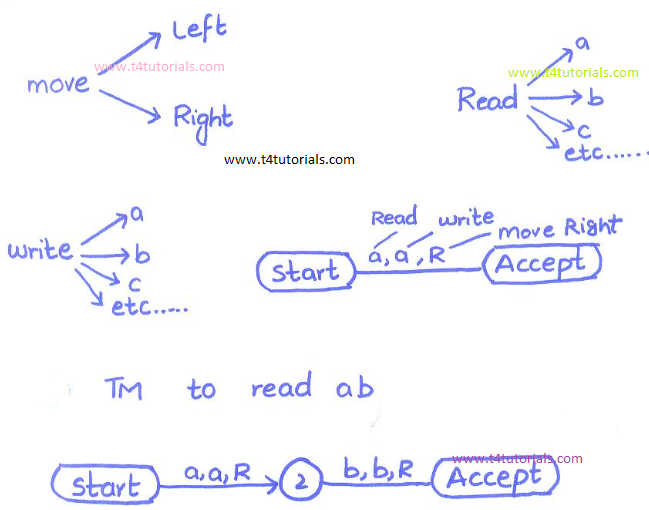
Explanation of diagram:
There is in one little part of a Turing machine in the last figure. Let’s explain it; Start state: To start the machine a,a,R: Read a from input tape, Write a and then move one cell right on input tape. b,b,R: Read b from input tape, Write b, and then move one cell right on input tape. Accept: Machine successfully accept the string and Halts(Finish/complete).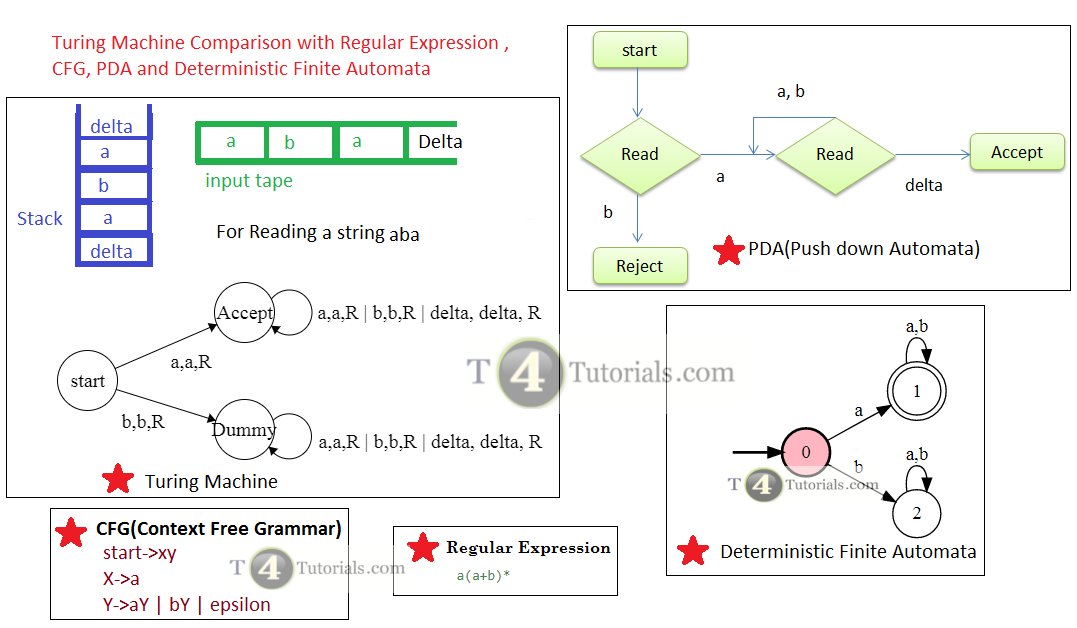
Read More Examples of Turing Machine
- Turing Machine to copy a string: with animations
- Turing Machine of numbers divisible by 3: with animations
- Turing machine for anbncn: with animations
-
Turing machine of two equal binary strings: with animations
-
Turing Machine to Accepts palindromes: with animations
-
Turing machine for a’s followed by b’s then c’s where the number of a’s multiplied by the number of b’s and equals to the number of c’s: with animations
-
Turing machine to Add two binary numbers: with animations
- Turing machine to Multiply two unary numbers: with animations
- Turing machine to Multiply two binary numbers: with animations
- Turing Machine for the complement of a string
- Turing Machine for the language of anbn where a=b.
- Turing Machine for a is less than b, ambn where a=b or m=n.
- Turing machine for the language of all those strings in which a is less than b
