Euclidean distance in data mining
What is the Euclidean distance?
Euclidean distance is a technique used to find the distance/dissimilarity among objects.
Example:
| Age | Marks | |
| Sameed | 10 | 90 |
| Shah zeb | 6 | 95 |
Formulae:
Euclidean distance (sameed, sameed) = SQRT ((X1 – X2)2 + (Y1 -Y2)2 ) = 0
Euclidean distance (sameed, sameed) = SQRT ((10 – 10)2 + (90 -90)2) = 0
Here note that (90-95) = -5 and when we take sqaure of a negative number then it will be a positive number. For example, (-5)2 = 25
Euclidean distance (sameed, shah zeb) = SQRT ((10 – 6)2 + (90 -95)2) = 6.40312
Euclidean distance (shah zeb, sameed) = SQRT ((10 – 6)2 + (90 -95)2) = 6.40312
Euclidean distance (sameed, sameed) = SQRT ((10 – 10)2 + (90 -90)2) = 0
Euclidean Distance is given below;
| Sameed | Shah zeb | |
| Sameed | 0 | 6.40312 |
| Shah zeb | 6.40312 | 0 |
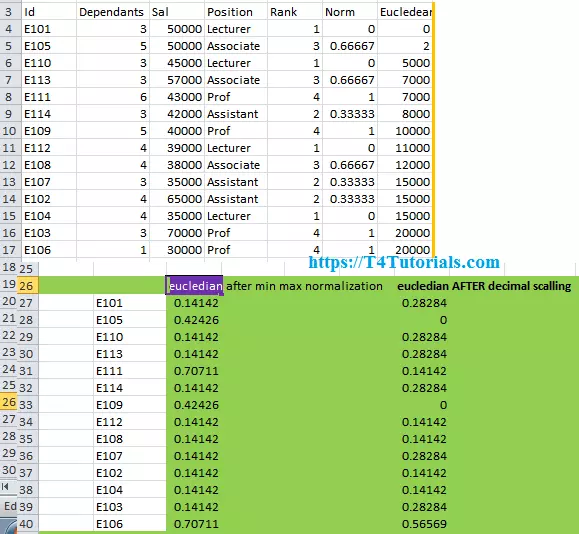
Download Excel File Calculations
This file contains the Euclidean distance of the data after the min-max, decimal scaling, and Z-Score normalization.
Euclidean distance after the min-max, decimal scaling, and Z-Score normalization
Let’s see the “Euclidean distance after the min-max, decimal scaling, and Z-Score normalization”.
Video Lecture
Next Similar Tutorials
- Proximity Measure for Nominal Attributes – Click Here
- Distance measure for asymmetric binary attributes – Click Here
- Distance measure for symmetric binary variables – Click Here
- Euclidean distance in data mining – Click Here Euclidean distance Excel file – Click Here
- Jaccard coefficient similarity measure for asymmetric binary variables – Click Here