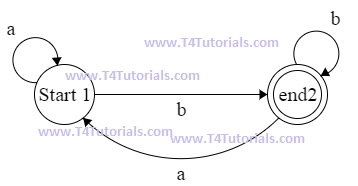
Finite automata for Language of all strings ending with b
Acceptable strings:
All strings of the following pattern must be accepted by the finite automata. For example, acceptable strings are b, ab, bb,bab, aaab, abab, babb,…… and all such strings with ending letter b. If any of the string that is not ending with b, and acceptable by finite automata machine, then the machine is wrong and wrong machine can read the invalid strings. Invalid strings are strings that are part of the language.
Rejectable strings:
All strings of the following pattern must not be accepted by the finite automata. For example, rejectable strings are a, ba, aa,bba, abaa,abba, baba,…… and all such strings with ending letter other than b. If any of the string that is not ending with b, and acceptable by finite automata machine, then machine is wrong and wrong machine can read the invalid strings. Invalid strings are strings that are part of the language.
In other words, we can say that all acceptable strings(100%) that are part of the language must be accepted(100%) by finite automata machine and all rejectable strings(100%) that must not be the part of the language and are rejected (100%) by finite automata machine, then the machine is OK, otherwise machine is not OK.
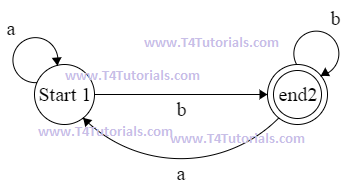In this example;
The machine can read many a’s when the machine starts. After reading a, the machine can read b and can move to a state(end2). Here from state(end2) machine have two options.
- The machine can read many b’s and remain stay on state(end2). Or
- The machine can read a and move to a state(start1).
Here, we can see that machines can pick the alphabet of its own choice but all the strings machine reads are part of our defined language “Language of all strings ending with b”.
The machine can finish its execution at the ending state and the ending state is stated (end2).
List of 100+ Important Deterministic Finite Automata
