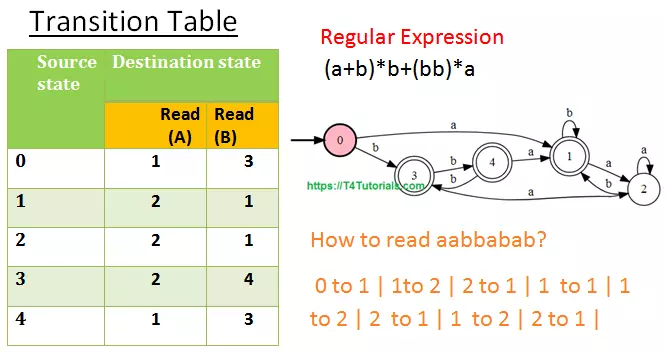
Let us see the Deterministic finite state machine Exercises solutions. In this tutorial, we will draw a DFA for the Regular Expression of (a+b)*b+(bb)*a.
Explanation of Strings of the langugage
- 2 Accepted strings of length 1 = {b,a no more possible string}
- 2 Accepted strings of length 2 = {ab , bb, … and many more similar strings }
- 2 Accepted strings of length 5 = {aaabb, bbbba,… and many more similar strings}
- 2 Accepted strings of length 8 = {aabbabab, bababbab, … and many more similar strings }
- 2 Accepted strings of length 10 = {aaaaababab , ababababab , … and many more similar strings }
- 2 Accepted strings of length 15 = { aaaaabbaababaab, bbbbbbbbbbbbbba , … and many more similar strings }
- 2 Accepted strings of length 20 = { aaaabbbbbbababababbb , abbbbbaaaabbabbaabab , … and many more similar strings }
- 2 Accepted strings of length 25 = { aaaaaaaaaabbbbbbaaaaaaaab , bbbbbbbbbbbbbbbbbbbbbbbba , … and many more similar strings }
- and many more similar strings
How to read b?
0 to 3
How to read a?
0 to 1
How to read ab?
0 to 1 | 0 to 3
How to read bb?
0 to 3 | 3 to 4
How to read aaabb ?
0 to 1 |1 to 2 |2 to 2 | 2 to 1 | 1 to 1 |
How to read bbbba ?
0 to 3 |3 to 4 | 4 to 3 | 3 to 4 | 4 to 1 |
How to read aabbabab?
0 to 1 | 1to 2 | 2 to 1 | 1 to 1 | 1 to 2 | 2 to 1 | 1 to 2 | 2 to 1 |
How to read bababbab?
0 to 3 | 3 to 2 | 2 to 1| 1 to 2 | 2 to 1 | 1 to 1 | 1 to 2 | 2 to 1 |
How to read aaaaababab?
0 to 1 | 1 to 2 | 2 to 2| 2 to 2 | 2 to 2 | 2 to 1 | 1 to 2 | 2 to 1 |1 to 2 | 2 to 1 |
How to read ababababab?
0 to 1 | 1 to 1 | 1 to 2| 2 to 1 | 1 to 2 | 2 to 1 | 1 to 2 | 2 to 1 |1 to 2 | 2 to 1 |
How to read aaaaabbaababaab?
0 to 1 | 1 to 2| 2 to 2| 2 to 2 | 2 to 2 | 2 to 1 | 1 to 1 | 1 to 2 |2 to 2 | 2 to 1 | 1 to 2 | 2 to 1 | 1 to 2 |2 to 2 | 2 to 1 |
How to read bbbbbbbbbbbbbba?
0 to 3 | 3 to 4 | 4 to 3| 3 to 4 | 4 to 3 | 3 to 4 | 4 to 3 | 3 to 4 |4 to 3 | 3 to 4 |4 to 3 | 3 to 4| 4 to 3 | 3 to 4 | 4 to 1 |
How to read aaaabbbbbbababababbb?
0 to 1 | 1 to 2 | 2 to 2| 2 to 2 | 2 to 1 |1 to 1 | 1 to 1| 1 to 1 | 1 to 1 | 1 to 1 | 1 to 2 | 2 to 1 |1 to 2 | 2 to 1 |1 to 2 | 2 to 1 |1 to 2 | 2 to 1 | 1 to 1 | 1 to 1 |
How to read abbbbbaaaabbabbaabab ?
0 to 1 | 1 to 1 | 1 to 1| 1 to 1 | 1 to 1 | 1 to 1 | 1 to 2 | 2 to 2 |2 to 2 | 2 to 2 |2 to 1 | 1 to 1| 1 to 2 | 2 to 1 | 1 to 1 | 1 to 2 | 2 to 2 |2 to 1 | 1 to 2 |2 to 1 |
How to read aaaaaaaaaabbbbbbaaaaaaaab?
0to 1 | 1 to 2 | 2 to 2| 2 to 2| 2 to 2| 2 to 2| 2 to 2| 2 to 2| 2 to 2| 2 to 2| 2 to 1| 1 to 1| 1 to 1 | 1 to 1 | 1 to 1 | 1 to 1 | 1 to 2 | 2 to 2| 2 to 2| 2 to 2| 2 to 2| 2 to 2| 2 to 2| 2 to 2| 2 to 1|
How to read bbbbbbbbbbbbbbbbbbbbbbbba?
0 to 3 | 3 to 4 | 4 to 3| 3 to 4 | 4 to 3 | 3 to 4 | 4 to 3 | 3 to 4 |4 to 3 | 3 to 4 |4 to 3 | 3 to 4| 4 to 3 | 3 to 4 |4 to 3 | 3 to 4| 4 to 3 | 3 to 4 |4 to 3 | 3 to 4| 4 to 3 | 3 to 4 | 4 to 3| 3 to 4 | 4 to 1 |
Video Lecture
List of 100+ Important Deterministic Finite Automata
I welcome to all of you if you want to discuss about any topic. Researchers, teachers and students are allowed to use the content for non commercial offline purpose. Further, You must use the reference of the website, if you want to use the partial content for research purpose.
- List of Public service commissions - August 31, 2020
- Comparison of fee structure of Pakistani Universities - June 1, 2020
- Past Guess Paper of Auditing - May 12, 2020