DFA in Theory of Computation and Automata

Regular Expression

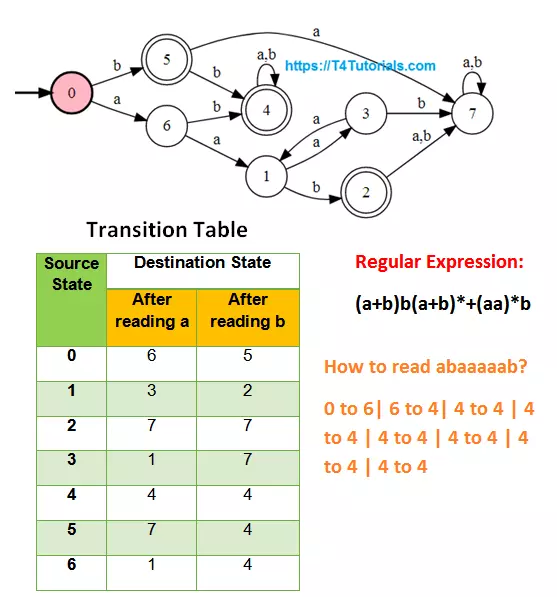
(a+b)b(a+b)*+(aa)*b  

Strings of DFA

• Accepted strings of length 1={b, no more possible string}
• Accepted strings of length 2={ab, bb, no more possible string }
• Accepted strings of length 5={abaaa, bbbba, …… and many more similar strings }
• Accepted strings of length 8={abaaaaab, bbaababa, …… and many more similar strings }
• Accepted strings of length 10={ababbbaaaa, bbbbbbbbba, …… and many more similar strings }
• Accepted strings of length 15={aaaaaaaaaaaaaab, bbaaaaaabbbabab, …… and many more similar strings }
• Accepted strings of length 20={abaaabababababbbaaaba, bbababababababababab, …… and many more similar strings }
• Accepted strings of length 25={aaaaaaaaaaaaaaaaaaaaaaab, bbaaaaaaaaaaaaaaaaaaaaaaa, …… and many more similar strings }
• And many more similar strings

How to read strings from DFA?

How to read b?

0 to 5

How to read ab?

0 to 6| 6 to 4

How to read bb?

0 to 5| 5 to 4

How to read abaaa?

0 to 6| 6 to 4 | 4 to 4| 4 to 4| 4 to 4

How to read bbbba?

0 to 5| 5 to 4| 4 to 4 | 4 to 4 | 4 to 4

How to read abaaaaab?

0 to 6| 6 to 4| 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4

How to read bbaababa?

0 to 5| 5 to 4| 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4

How to read ababbbaaaa?

0 to 6| 6 to 4| 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4

How to read bbbbbbbbba?

0 to 5| 5 to 4| 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4

How to read aaaaaaaaaaaaaab?

0 to 6| 6 to 1| 1 to 3| 3 to 1| 1 to 3| 3 to 1|1 to 3| 3 to 1|1 to 3| 3 to 1|1 to 3| 3 to 1|1 to 3| 3 to 1| 1 to 2

How to read bbaaaaaabbbabab?

0 to 5| 5 to 4| 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4| 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4

How to read abaaabababababbbaaaba?

0 to 6| 6 to 4| 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4| 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4| 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4

How to read bbababababababababab?

0 to 5| 5 to 4| 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4| 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4| 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4

How to read aaaaaaaaaaaaaaaaaaaaaaaab?

0 to 6| 6 to 1| 1 to 3| 3 to 1| 1 to 3| 3 to 1|1 to 3| 3 to 1|1 to 3| 3 to 1|1 to 3| 3 to 1|1 to 3| 3 to 1|1 to 3| 3 to 1|1 to 3| 3 to 1|1 to 3| 3 to 1|1 to 3| 3 to 1|1 to 3| 3 to 1| 1 to 2

How to read bbaaaaaaaaaaaaaaaaaaaaaaaa?

0 to 5| 5 to 4| 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4| 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4| 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4| 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4 | 4 to 4

Finite Automata Exercise Solution

Here I am showing you a list of some more important Deterministic Finite Automata used in the theory of automata and theory of computation.

1. DFA for  (a+b)* (a+b)a .
2. DFA for (bb)*(aa)* .
3. DFA for  b+a(a+b)*+a.
4. DFA for (a+b)*b+(bb)*a.
5. DFA for bb+a(a+b)*+aa.
6. DFA for  a(a+b)*+bb(a)* .
7. DFA for  a(a+b)b*+bb(a)*.
8. DFA for  b(aa)*a+a(bb)*b.
9. DFA for a+a(aa+b)*(aa)b.
10. DFA for a+a(aa+b)*+(aa)b.
11. DFA for (a+b)b(a+b)*+(aa)*b.
12. FA for strings starting with a and ending with a.
13. FA for the language of all those strings starting with a.
14. FA for the language of all those strings containing aa as a substring.
15. DFA for the language of all those strings starting and ending with the same letters.
16. DFA for the language of all those strings starting and ending with different letters.
17. DFA for the language of all those strings having double 0 or double 1.
18. DFA for the language of all those strings starting and ending with b.
19. DFA for ending with b.
20. DFA for the string of even A’s and even b’s.
21. DFA for the regular expression of  a(a+b)*+(bb)+a(ba)*+aba+bb*(a+b)*.
22. RegExp and DFA for strings having triple a’s or triple b’s.