Let us begin with Deterministic Finite Automata (FA) Examples with a transition table and detailed explanation.
The given DFA is for the Regular expression of (bb)*(aa)*.
- 2 Accepted strings of length 1= {No String Exist}
- 2 Accepted strings of length 2= {bb, aa}
- 2 Accepted strings of length 5= {No String Exist}
- 2 Accepted strings of length 8= {bbbbaaaa, bbbbbbbb, …. and many more similar strings.}
- 2 Accepted strings of length 10= {bbbbbbaaaa, bbaaaaaaaa, …. and many more similar strings.}
- 2 Accepted strings of length 15= {No String Exist}
- 2 Accepted strings of length 20= {bbbbbbbbbbbbbbbbaaaa, bbbbbbbbbbaaaaaaaaaa, …. and many more similar strings. }
- 2 Accepted strings of length 25= {No String Exist}
- and many more similar strings
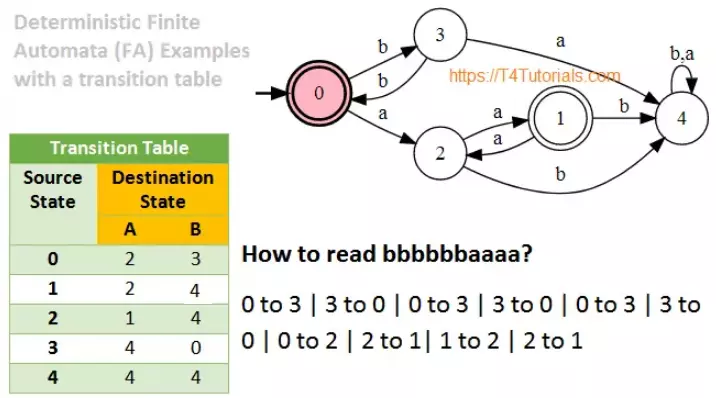
How to read bb?
0 to 3 | 3 to 0
How to read aa?
0 to 2 | 2 to 1
How to read bbbbaaaa?
0 to 3 | 3 to 0 |0 to 3 |3 to 0| 0 to 2 | 2 to 1| 1 to 2 | 2 to 1
How to read bbbbbbbb?
0 to 3 | 3 to 0 | 0 to 3 | 3 to 0 | 0 to 3 | 3 to 0 | 0 to 3 | 3 to 0
How to read bbbbbbaaaa?
0 to 3 | 3 to 0 | 0 to 3 | 3 to 0 | 0 to 3 | 3 to 0 | 0 to 2 | 2 to 1| 1 to 2 | 2 to 1
How to read bbaaaaaaaa?
0 to 3 | 3 to 0 | 0 to 2 | 2 to 1| 1 to 2 | 2 to 1 | 1 to 2| 2 to 1 | 1 to 2 | 2 to 1
How to read bbbbbbbbbbbbbbbbaaaa?
0 to 3 | 3 to 0 | 0 to 3 | 3 to 0 | 0 to 3 | 3 to 0 | 0 to 3 | 3 to 0 |0 to 3 | 3 to 0 | 0 to 3 | 3 to 0 | 0 to 3 | 3 to 0 | 0 to 3 | 3 to 0 | 0 to 2 | 2 to 1| 1 to 2 | 2 to 1
How to read bbbbbbbbbbaaaaaaaaaa?
0 to 3 | 3 to 0 | 0 to 3 | 3 to 0 | 0 to 3 | 3 to 0 | 0 to 3 | 3 to 0 |0 to 3 | 3 to 0 | 0 to 2 | 2 to 1| 1 to 2 | 2 to 1 | 1 to 2| 2 to 1 | 1 to 2 | 2 to 1 | 1 to 2 | 2 to 1
List of 100+ Important Deterministic Finite Automata
