Regular Expression for strings having at least one double 0 or double 1

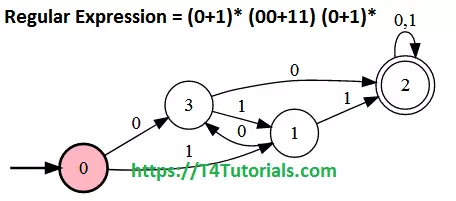
Let us see the Regular Expression for strings having at least one double 0 or double 1 defined over {0,1}.

Rule

All strings having at least one double 0 or double 1 must be accepted and all other strings must be rejected by our Regular Expression.

Regular Expression = (0+1)* (00+11) (0+1)*

DFA of Language having at least one double 0 or double 1

Reject able strings (not part of the language)

These strings are not part of the given language and must be rejected by our Regular Expression.

• 3 strings of length 1 = {1, 0, no more string}
• 3 strings of length 2 = {01, 10, no more string}
• 3 strings of length 3= {101,010, no more string}
• 3 strings of length 4 = {1010, 0101, no more string}
• 3 strings of length 7 = {0101010, 1010101, no more string}
• 3 strings of length 10 = {1010101010, 0101010101, no more string}
• 3 strings of length 15 = {101010101010101, 010101010101010, no more strings}
• 3 strings of length 20 = {01010101010101010101, 10101010101010101010, no more string}
  3 strings of length 25 = {1010101010101010101010101, 0101010101010101010101010, no more string}
• Many more similar strings.

Acceptable strings (part of the language)

These strings are part of the given language and must be accepted by our Regular Expression.

• 3 strings of length 1 = {no string}
• 3 strings of length 2 = {00, 11, no more string}
• 3 strings of length 3= {000,111,001, and many more similar strings}
• 3 strings of length 4 = {0000, 1111, 0110, and many more similar strings}
• 3 strings of length 7 = {0010001, 1101110, 0100001, and many more similar strings}
• 3 strings of length 10 = {0011001010, 1010111000, 0111110010, and many more similar strings}
• 3 strings of length 15 = {000001111100110, 110011001011001, 111111111110010, and many more similar strings}
• 3 strings of length 20= {00001111001111000010, 11001111000001111001, 10101010101101101001, and many more similar strings}
  3 strings of length 25= {0010101000110101110011000, 1111100000100100110100001, 0101010101010110110000001, and many more similar strings}
• Many more similar strings.

---

Regular Expression for strings having at least one double a or double b

Let us see the Regular Expression for strings having at least one double a or double b defined over {a,b}.

Rule

All strings having at least one double a or double b must be accepted and all other strings must be rejected by our Regular Expression.

Regular Expression = (a+b)* (aa+bb) (a+b)*

Reject able strings (not part of the language)

These strings are not part of the given language and must be rejected by our Regular Expression.

• 3 strings of length 1 = {b, a, no more string}
• 3 strings of length 2 = {ab, ba, no more string}
• 3 strings of length 3= {bab,aba, no more string}
• 3 strings of length 4 = {baba, abab, no more string}
• 3 strings of length 7 = {abababa, bababab, no more string}
• 3 strings of length 10 = {bababababa, ababababab, no more string}
• 3 strings of length 15 = {bababababababab, abababababababa, no more strings}
• 3 strings of length 20 = {abababababababababab, babababababababababa, no more string}
  3 strings of length 25 = {babababababababababababab, ababababababababababababa, no more string}
• Many more similar strings.

Acceptable strings (part of the language)

These strings are part of the given language and must be accepted by our Regular Expression.

• 3 strings of length 1 = {no string}
• 3 strings of length 2 = {aa, bb, no more string}
• 3 strings of length 3= {aaa,bbb,aab, and many more similar strings}
• 3 strings of length 4 = {aaaa, bbbb, abba, and many more similar strings}
• 3 strings of length 7 = {aabaaab, bbabbba, abaaaab, and many more similar strings}
• 3 strings of length 10 = {aabbaababa, bababbbaaa, abbbbbaaba, and many more similar strings}
• 3 strings of length 15 = {aaaaabbbbbaabba, bbaabbaababbaab, bbbbbbbbbbbaaba, and many more similar strings}
• 3 strings of length 20= {aaaabbbbaabbbbaaaaba, bbaabbbbaaaaabbbbaab, babababababbabbabaab, and many more similar strings}
  3 strings of length 25= {aabababaaabbababbbaabbaaa, bbbbbaaaaabaabaabbabaaaab, abababababababbabbaaaaaab, and many more similar strings}
• Many more similar strings.

More Examples of Regular Expression 

1. Regular Expression for no 0 or many triples of 0’s and many 1 in the strings.
2. RegExp for strings of one or many 11 or no 11.
3. A regular expression for ending with abb
4. A regular expression for all strings having 010 or 101.
5. Regular expression for Even Length Strings defined over {a,b}
6. Regular Expression for strings having at least one double 0 or double 1.
7. Regular Expression of starting with 0 and having multiple even 1’s or no 1.
8. Regular Expression for an odd number of 0’s or an odd number of 1’s in the strings.
9. Regular Expression for having strings of multiple double 1’s or null.
10. Regular Expression (RE) for starting with 0 and ending with 1.
11. RE for ending with b and having zero or multiple sets of aa and bb.
12. A regular expression of the second last symbol is 1.
13. RE for starting with 1 having zero or multiple even 1’s.
14. Regular Expression for multiple a’s and multiple b’s.
15. RE for exactly single 1 many 0’s |exactly single a many b.
16. A regular expression for strings starting with aa and ending with ba.
17. A regular expression for the language of all consecutive even length a’s.
18. A regular expression for the language of all odd-length strings
19. A regular expression for the language of all even length strings but ends with aa.
20. A regular expression for the language of an odd number of 1s.
21. A regular expression for the language of even length strings starting with a and ending with b in theory of automata.
22. A regular expression for the language of all even length strings but starts with a.
23. A Regular Expression for the Language of all strings with an even number of 0’s or even number of 1’s.
24. A regular expression for the language of all those strings end with abb.
25. A regular expression for string having must 010 or 101.
26. Regular expression of  strings begin with 110
    Regular expression of  strings begin and end with 110
    Regular expression of strings containing exactly three consecutive 1’s.
27. A Regular Expression of all strings divisible by 4.
28. A Regular Expression Strings that does not contain substring 110.

Tutorial: Regular Expression

A detailed tutorial of the regular expression is here in the link of regular expression tutorial. This page contains the practice questions of regular expressions with solutions.

Tutorial covering the topics

• Give a regular expression.
• Describe the strings of the regular expression.
• write a regular expression.
• create all strings from regular expression.
• Generate all strings from regular expression.
• Extract all strings from regular expression.
• Find all strings from regular expression.
• Examples of regular expression.