RE for ending with b and having zero or multiple pairs of aa and bb

Regular Expression = (aa+bb)*b

DFA for strings ending with b and having zero or multiple pairs of aa and bb

---

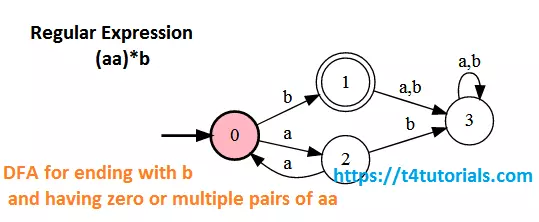
RE for ending with b and having zero or multiple pairs of aa but no two b’s

Regular Expression = (aa)*b

DFA for strings ending with b and having zero or multiple pairs of aa but no two b’s

---

RE for ending with b and having one or multiple pairs of aa

Regular Expression  = (aa)⁺ b

---

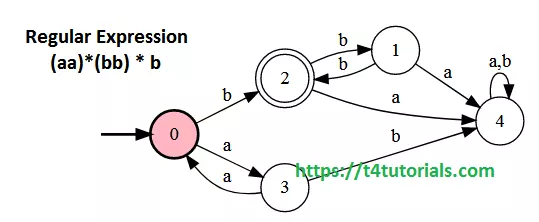
 RE for ending with b and having zero or multiple pairs of aa and bb, but no pair of aa after the pair of bb

RE for ending with b and having zero or multiple sets of aa and bb, but no pair of aa after the pair of bb

Rule

Regular Expression (RE) for ending with b and having zero or multiple sets of aa and bb must be accepted and all other strings must be rejected by our Regular Expression.

Regular Expression = (aa)*(bb) * b

DFA of strings ending with b and having zero or multiple sets of aa and bb, but no pair of aa after the pair of bb

Accepted Strings (part of the language)

These strings are not part of the given language and must be rejected by our Regular Expression.

• 3 strings of length 01 = {b,no more strings }
• 3 strings of length 02 = { no string exist}
• 3 strings of length 03= {aab, bbb, no more strings}
• 3 strings of length 04= { no string exist}
• 3 strings of length 05 = {aabbb, aaaab,bbbbb no more strings }
• 3 strings of length 06 = { no string exist }
• 3 strings of length 07 = {aaaaaab, aabbbbb, bbbbbbb, and many more similar strings }
• 3 strings of length 08= { no string exist}
• 3 strings of length 09 = {aaaaaabbb, aaaabbbbb, aaaaaaaab, and many more similar strings }
• 3 strings of length 10= { no string exist }
• Mmany more similar strings

Rejected Strings (not part of the language) These strings are part of the given language and must be accepted by our Regular Expression.

• 3 strings of length 01 = {a, no more strings}
• 3 strings of length 02 = {ab, bb, aa}
• 3 strings of length 03 = {aaa, bba, abb}
• 3 strings of length 04 = {aaab, bbbb, aabb}
• 3 strings of length 05= {abbbb, aaabb, aaaaa, and many more similar strings }
• 3 strings of length 06 = {aaaaab, aabbbb,bbbbbb, and many more similar  strings }
• 3 strings of length 07 = {aaaaaaa, abbbbbb, aaaaabb, and many more similar strings }
• 3 strings of length 08 = {aaaabbbb, bbbbbbbb, aabbbbbb, and many more similar strings }
• 3 strings of length 09 = {aaabbbbbb, abbbbbbbb,aaaaabbbb, and many more similar strings }
• 3 strings of length 10 = {aaaabbbbbb,aaabbbbbbb, aabbbbbbbb, and many more similar strings }

More Examples of Regular Expression 

1. Regular Expression for no 0 or many triples of 0’s and many 1 in the strings.
2. RegExp for strings of one or many 11 or no 11.
3. A regular expression for ending with abb
4. A regular expression for all strings having 010 or 101.
5. Regular expression for Even Length Strings defined over {a,b}
6. Regular Expression for strings having at least one double 0 or double 1.
7. Regular Expression of starting with 0 and having multiple even 1’s or no 1.
8. Regular Expression for an odd number of 0’s or an odd number of 1’s in the strings.
9. Regular Expression for having strings of multiple double 1’s or null.
10. Regular Expression (RE) for starting with 0 and ending with 1.
11. RE for ending with b and having zero or multiple sets of aa and bb.
12. A regular expression of the second last symbol is 1.
13. RE for starting with 1 having zero or multiple even 1’s.
14. Regular Expression for multiple a’s and multiple b’s.
15. RE for exactly single 1 many 0’s |exactly single a many b.
16. A regular expression for strings starting with aa and ending with ba.
17. A regular expression for the language of all consecutive even length a’s.
18. A regular expression for the language of all odd-length strings
19. A regular expression for the language of all even length strings but ends with aa.
20. A regular expression for the language of an odd number of 1s.
21. A regular expression for the language of even length strings starting with a and ending with b in theory of automata.
22. A regular expression for the language of all even length strings but starts with a.
23. A Regular Expression for the Language of all strings with an even number of 0’s or even number of 1’s.
24. A regular expression for the language of all those strings end with abb.
25. A regular expression for string having must 010 or 101.
26. Regular expression of  strings begin with 110 Regular expression of  strings begin and end with 110 Regular expression of strings containing exactly three consecutive 1’s.
27. A Regular Expression of all strings divisible by 4.
28. A Regular Expression Strings that does not contain substring 110.

Tutorial: Regular Expression

A detailed tutorial of the regular expression is here in the link of regular expression tutorial. This page contains the practice questions of regular expressions with solutions. Tutorial covering the topics

• Give a regular expression.
• Describe the strings of the regular expression.
• write a regular expression.
• create all strings from regular expression.
• Generate all strings from regular expression.
• Extract all strings from regular expression.
• Find all strings from regular expression.
• Examples of regular expression.