Closure Properties of Regular Expressions

• Union
• Intersection
• concatenation
• Kleene closure
• Complement

Union Of Regular Expression With Examples

  If RE1 and RE2 are regular, then RE1 union RE2 is also a regular expression. This can be written as;

• RE1 | RE2
• RE1 U RE2
• RE1 + RE2

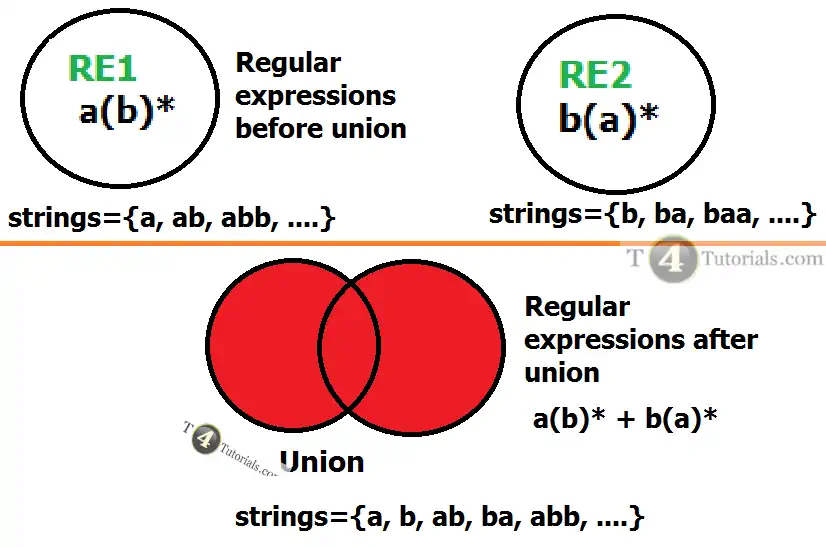
Examples of Union Operation Of Regular Expression

Example 1 RE1= a(b)* RE2 = b(a)* RE1 + RE2= a(b)* + b(a)* Result: Regular expressions are closed under union operation.

---

Example 2 Regular expression 1:  a Regular expression 2:  b Regular expression 1 + Regular expression 2 = a+b

---

More examples of Union as a closure property Of Regular Expression

Regular expression 1:  a(a) Regular expression 2:  b(a+b) Regular expression 1 + Regular expression 2 = a(a)+ b(a+b)   Regular expression 1:  b(aa+b) Regular expression 2:  b(aa+b) Regular expression 1 + Regular expression 2 = b(aa+b) + b(aa+b)   Regular expression 1:  a(aa+bb)* Regular expression 2:  b(aa) Regular expression 1 + Regular expression 2 = a(aa+bb)*+ b(aa)  

Intersection Of Regular Expression With Examples

If RE1 and RE2 are regular, then RE1 ∩  RE2 is also a regular expression.

Examples of Intersection Operation Of Regular Expression

Example 1:

RE1 = b(b*) RE2 = (bb)* RE1 ∩ RE2=  bb(bb)* Explanation: L₁ = { b,bb, bbb, bbbb, ….} (Strings of all possible lengths of b without Null) L₂ = { ε, bb, bbbb, bbbbbb,…….} (Strings of even length of b including Null) L₁ ∩ L₂ = { bb, bbbb, bbbbbb,…….} (Strings of even length of b excluding Null)

Concatenation Of Regular Expression With Examples

If RE1 and RE2 are regular, then RE1.RE2 is also a regular expression.

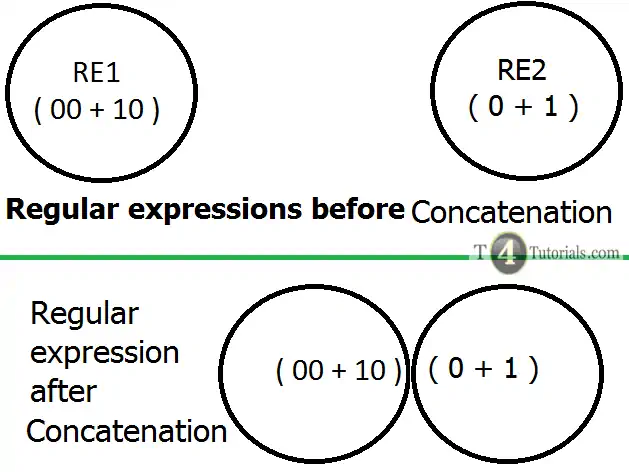
Examples of Concatenation Operation Of Regular Expression

Example 1:

Regular Expression 1 = ( 00 + 10 )

strings are = {00, 10 only}

Regular Expression 2 = ( 0 + 1 )

strings are = {0, 1 only}

Regular Expression 1 ◦Regular Expression 2 = ( 00 + 10 )( 0 + 1 )

strings are = {000, 001, 100, 101}

Example 2:

Regular Expression 1 = (0+1)*0

set of strings ending in 0

Regular Expression 2 = 01(0+1)*

set of strings beginning with 01

Regular Expression 1 ◦ Regular Expression 2 = 01(0+1)* (0+1)*0 which can be written in more optimized way as;

01(0+1)*0

 

Regular Expression Basics and rules