- 3, 82
- 4, 81
- 5, 80
- 6, 79, etc…
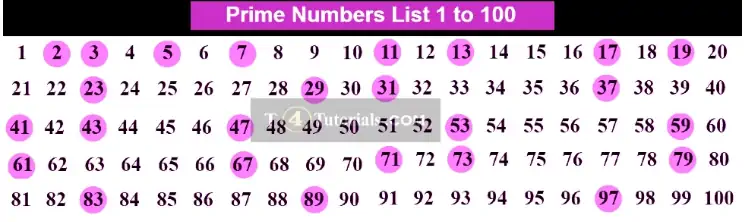
List of prime numbers
All prime numbers are illustrated with pink color circles.Sum of Prime number with classes
Let’s see a little demo with the C++ program that works on sum of prime numbers.|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
#include<iostream> using namespace std; class T4Tutorials { protected : int n, i, flg1,flg2,flg3,j; public : int checK() { flg1=1,flg2=1,flg3=0; cout<<"Input a positive integer: "; cin>>n; for(i=3; i<=n/2; i++) { flg1=1; flg2=1; for(j=2; j<i; j++) { if(i%j==0) { flg1=0;j=i;} } for(j=2; j<n-i; j++) { if((n-i)%j==0) { flg2=0;j=n-i;} } if(flg1==1 && flg2==1) { printf("%d = %d + %d \n",n,i,n-i); flg3=1;} } if(flg3==0) {printf("\n%d can not be expressed as sum of two prime numbers.\n\n",n);} } }; int main() { T4Tutorials a; a.checK(); } |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
#include<iostream> using namespace std; class T4Tutorials { protected : int n, i; }; class T4Tutorials_child { protected : int n, i, X,Y,Z,j; public : int checK() { X=1,Y=1,Z=0; cout<<"\n\nCheck Whether a Number can be Express as Sum of Two Prime Numbers:\n "; cout<<"Input a positive integer: "; cin>>n; for(i=3; i<=n/2; i++) { X=1; Y=1; for(j=2; j<i; j++) { if(i%j==0) { X=0;j=i;} } for(j=2; j<n-i; j++) { if((n-i)%j==0) { Y=0;j=n-i;} } if(X==1 && Y==1) { printf("%d = %d + %d \n",n,i,n-i); Z=1;} } if(Z==0) {printf("\n%d can not be expressed as sum of two prime numbers.\n\n",n);} } }; int main() { T4Tutorials_child a; a.checK(); } |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
#include<iostream> using namespace std; class T4Tutorials1 { protected : int n, i; }; class T4Tutorials2 { protected : int flg3,j; }; class T4Tutorials3 : public T4Tutorials2 , public T4Tutorials1 { protected : int flg1,flg2,flg3,j; public : int checK() { flg1=1,flg2=1,flg3=0; cout<<"\n\nCheck Whether a Number can be Express as Sum of Two Prime Numbers:\n "; cout<<"Input a positive integer: "; cin>>n; for(i=3; i<=n/2; i++) { /*---------- check for prime---------------*/ flg1=1; flg2=1; for(j=2; j<i; j++) { if(i%j==0) { flg1=0;j=i;} } for(j=2; j<n-i; j++) { if((n-i)%j==0) { flg2=0;j=n-i;} } if(flg1==1 && flg2==1) { printf("%d = %d + %d \n",n,i,n-i); flg3=1;} } if(flg3==0) {printf("\n%d can not be expressed as sum of two prime numbers.\n\n",n);} } }; int main() { T4Tutorials3 a; a.checK(); } |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
#include<iostream> using namespace std; class T4Tutorials_grandFather { protected : int n, i; }; class T4Tutorials_Father : public T4Tutorials_grandFather { protected : int flg3,j; }; class T4Tutorials3 : public T4Tutorials_Father { protected : int flg1,flg2,flg3,j; public : int checK() { flg1=1,flg2=1,flg3=0; cout<<"\n\nCheck Whether a Number can be Express as Sum of Two Prime Numbers:\n "; cout<<"Input a positive integer: "; cin>>n; for(i=3; i<=n/2; i++) { /*---------- check for prime---------------*/ flg1=1; flg2=1; for(j=2; j<i; j++) { if(i%j==0) { flg1=0;j=i;} } for(j=2; j<n-i; j++) { if((n-i)%j==0) { flg2=0;j=n-i;} } if(flg1==1 && flg2==1) { printf("%d = %d + %d \n",n,i,n-i); flg3=1;} } if(flg3==0) {printf("\n%d can not be expressed as sum of two prime numbers.\n\n",n);} } }; int main() { T4Tutorials3 a; a.checK(); } |