| Comparison | Recursive Language | Recursively enumerable language |
| Also Known as | Turing decidable languages | Turing recognizable languages |
| Definition | In Recursive Languages, the Turing machine accepts all valid strings that are part of the language and rejects all the strings that are not part of a given language and halt. | In Recursively enumerable languages, the Turing machine accepts all valid strings that are part of the language and rejects all the strings that are not part of the given language but do not halt and starts an infinite loop. |
| States | (1) Halt and accept
(2) Halt and Reject
|
(3) Halt and accept (4) Halt and Reject (5) Never Halt (Infinite loop) |
| Loop | Finite Loop | Infinite loops of machine are possible |
| Halting | Halting Turing Machine | Non Halting Turing Machine |
| Accept/ Reject | Accept (Turing machine) = L Reject (Turing machine) = L‘ Loop (Turing machine) = φφ φ = null φ = null |
Accept (Turing machine) = LReject (Turing machine) + Loop (Turing machine) = L’ |
| Closed under | Closed under all except homomorphism, substitution, GSM mapping, and rational transduction | Closed under all except set difference, and complementation. |
| context-sensitive language | RE languages or type-0 language |
FAQ about Recursive languages closure properties
Properties of Recursively enumerable languages
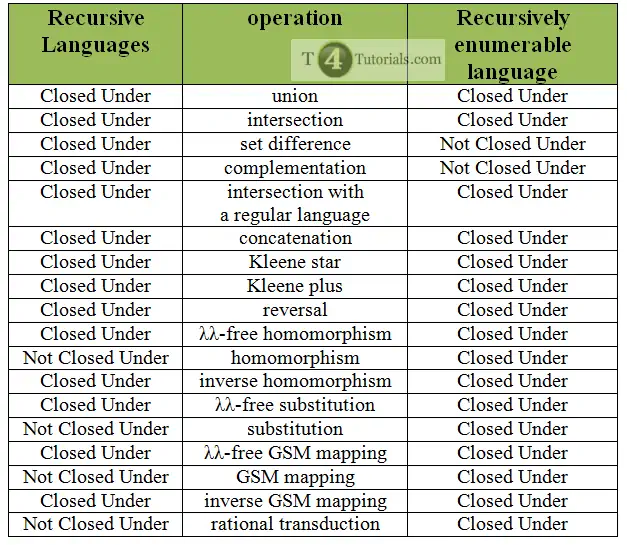
- Recursive Languages Closed Under union.
- Recursive Languages Closed Under intersection.
- Recursive Languages Closed Under set difference.
- Recursive Languages Closed Undercomplementation.
- Recursive Languages Closed Under intersection with a regular language.
- Recursive Languages Closed Under concatenation.
- Recursive Languages Closed Under Kleene star.
- Recursive Languages Closed Under Kleene plus.
- Recursive Languages Closed Under reversal.
- Recursive Languages Closed Under λλ-free homomorphism.
- Recursive Languages Recursive Languages Not Closed Under homomorphism.
- Recursive Languages Closed Under inverse homomorphism.
- λλ-free substitution Recursive Languages Closed Under λλ-free substitution.
- Recursive Languages Not Closed Under substitution.
- Recursive Languages Closed Under λλ-free GSM mapping.
- Recursive Languages Not Closed Under GSM mapping.
- Recursive Languages Closed Under inverse GSM mapping.
- Recursive Languages Not Closed Under rational transduction.
FAQ about Recursively Enumerable languages closure properties?
- Recursively enumerable languages Closed under union.
- Recursively enumerable languages Closed under intersection.
- Recursively enumerable languages Not Closed under set difference.
- Recursively enumerable languages Not Closed under complementation.
- Recursively enumerable languages Closed under intersection with a regular language.
- Recursively enumerable languages Closed under concatenation.
- Recursively enumerable languages Closed under Kleene star.
- Recursively enumerable languages Closed under Kleene plus.
- Recursively enumerable languages Closed under reversal.
- Recursively enumerable languages Closed under λλ-free homomorphism.
- Recursively enumerable languages Closed under homomorphism.
- Recursively enumerable languages Closed under inverse homomorphism.
- Recursively enumerable languages Closed under λλ-free substitution.
- Recursively enumerable languages Closed under substitution.
- Recursively enumerable languages Closed under λλ-free GSM mapping.
- Recursively enumerable languages Closed under GSM mapping.
- Recursively enumerable languages Closed under inverse GSM mapping.
- Recursively enumerable languages Closed under rational transduction.


