\[
\textbf{Matrix Addition Questions}
\]
\[
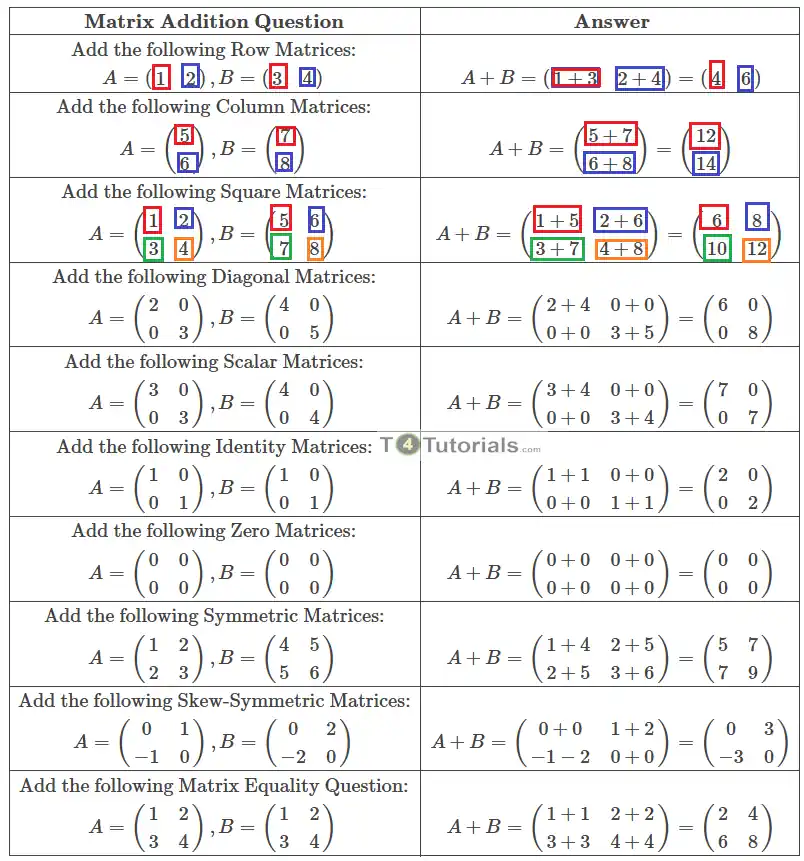
\textbf{Q1: Add the following Row Matrices:}
\]
\[
A = \begin{pmatrix} 1 & 2 \end{pmatrix}, \quad B = \begin{pmatrix} 3 & 4 \end{pmatrix}
\]
\[
\textbf{Q2: Add the following Column Matrices:}
\]
\[
A = \begin{pmatrix} 5 \\ 6 \end{pmatrix}, \quad B = \begin{pmatrix} 7 \\ 8 \end{pmatrix}
\]
\[
\textbf{Q3: Add the following Square Matrices:}
\]
\[
A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}, \quad B = \begin{pmatrix} 5 & 6 \\ 7 & 8 \end{pmatrix}
\]
\[
\textbf{Q4: Add the following Diagonal Matrices:}
\]
\[
A = \begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix}, \quad B = \begin{pmatrix} 4 & 0 \\ 0 & 5 \end{pmatrix}
\]
\[
\textbf{Q5: Add the following Scalar Matrices:}
\]
\[
A = \begin{pmatrix} 3 & 0 \\ 0 & 3 \end{pmatrix}, \quad B = \begin{pmatrix} 4 & 0 \\ 0 & 4 \end{pmatrix}
\]
\[
\textbf{Q6: Add the following Identity Matrices:}
\]
\[
A = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}, \quad B = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}
\]
\[
\textbf{Q7: Add the following Zero Matrices:}
\]
\[
A = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}, \quad B = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}
\]
\[
\textbf{Q8: Add the following Symmetric Matrices:}
\]
\[
A = \begin{pmatrix} 1 & 2 \\ 2 & 3 \end{pmatrix}, \quad B = \begin{pmatrix} 4 & 5 \\ 5 & 6 \end{pmatrix}
\]
\[
\textbf{Q9: Add the following Skew-Symmetric Matrices:}
\]
\[
A = \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}, \quad B = \begin{pmatrix} 0 & 2 \\ -2 & 0 \end{pmatrix}
\]
\[
\textbf{Q10: Add the following Matrix Equality Question:}
\]
\[
A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}, \quad B = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}
\]
Solution
\[
\textbf{Q1: Add the following Row Matrices:}
\]
\[
A = \begin{pmatrix} 1 & 2 \end{pmatrix}, \quad B = \begin{pmatrix} 3 & 4 \end{pmatrix}
\]
\[
\textbf{Solution:}
\]
\[
A + B = \begin{pmatrix} 1+3 & 2+4 \end{pmatrix} = \begin{pmatrix} 4 & 6 \end{pmatrix}
\]
\[
\textbf{Q2: Add the following Column Matrices:}
\]
\[
A = \begin{pmatrix} 5 \\ 6 \end{pmatrix}, \quad B = \begin{pmatrix} 7 \\ 8 \end{pmatrix}
\]
\[
\textbf{Solution:}
\]
\[
A + B = \begin{pmatrix} 5+7 \\ 6+8 \end{pmatrix} = \begin{pmatrix} 12 \\ 14 \end{pmatrix}
\]
\[
\textbf{Q3: Add the following Square Matrices:}
\]
\[
A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}, \quad B = \begin{pmatrix} 5 & 6 \\ 7 & 8 \end{pmatrix}
\]
\[
\textbf{Solution:}
\]
\[
A + B = \begin{pmatrix} 1+5 & 2+6 \\ 3+7 & 4+8 \end{pmatrix} = \begin{pmatrix} 6 & 8 \\ 10 & 12 \end{pmatrix}
\]
\[
\textbf{Q4: Add the following Diagonal Matrices:}
\]
\[
A = \begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix}, \quad B = \begin{pmatrix} 4 & 0 \\ 0 & 5 \end{pmatrix}
\]
\[
\textbf{Solution:}
\]
\[
A + B = \begin{pmatrix} 2+4 & 0+0 \\ 0+0 & 3+5 \end{pmatrix} = \begin{pmatrix} 6 & 0 \\ 0 & 8 \end{pmatrix}
\]
\[
\textbf{Q5: Add the following Scalar Matrices:}
\]
\[
A = \begin{pmatrix} 3 & 0 \\ 0 & 3 \end{pmatrix}, \quad B = \begin{pmatrix} 4 & 0 \\ 0 & 4 \end{pmatrix}
\]
\[
\textbf{Solution:}
\]
\[
A + B = \begin{pmatrix} 3+4 & 0+0 \\ 0+0 & 3+4 \end{pmatrix} = \begin{pmatrix} 7 & 0 \\ 0 & 7 \end{pmatrix}
\]
\[
\textbf{Q6: Add the following Identity Matrices:}
\]
\[
A = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}, \quad B = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}
\]
\[
\textbf{Solution:}
\]
\[
A + B = \begin{pmatrix} 1+1 & 0+0 \\ 0+0 & 1+1 \end{pmatrix} = \begin{pmatrix} 2 & 0 \\ 0 & 2 \end{pmatrix}
\]
\[
\textbf{Q7: Add the following Zero Matrices:}
\]
\[
A = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}, \quad B = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}
\]
\[
\textbf{Solution:}
\]
\[
A + B = \begin{pmatrix} 0+0 & 0+0 \\ 0+0 & 0+0 \end{pmatrix} = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}
\]
\[
\textbf{Q8: Add the following Symmetric Matrices:}
\]
\[
A = \begin{pmatrix} 1 & 2 \\ 2 & 3 \end{pmatrix}, \quad B = \begin{pmatrix} 4 & 5 \\ 5 & 6 \end{pmatrix}
\]
\[
\textbf{Solution:}
\]
\[
A + B = \begin{pmatrix} 1+4 & 2+5 \\ 2+5 & 3+6 \end{pmatrix} = \begin{pmatrix} 5 & 7 \\ 7 & 9 \end{pmatrix}
\]
\[
\textbf{Q9: Add the following Skew-Symmetric Matrices:}
\]
\[
A = \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}, \quad B = \begin{pmatrix} 0 & 2 \\ -2 & 0 \end{pmatrix}
\]
\[
\textbf{Solution:}
\]
\[
A + B = \begin{pmatrix} 0+0 & 1+2 \\ -1-2 & 0+0 \end{pmatrix} = \begin{pmatrix} 0 & 3 \\ -3 & 0 \end{pmatrix}
\]
\[
\textbf{Q10: Add the following Matrix Equality Question:}
\]
\[
A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}, \quad B = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}
\]
\[
\textbf{Solution:}
\]
\[
A + B = \begin{pmatrix} 1+1 & 2+2 \\ 3+3 & 4+4 \end{pmatrix} = \begin{pmatrix} 2 & 4 \\ 6 & 8 \end{pmatrix}
\]
[latex]
\[
\textbf{Matrix Addition Questions and Answers}
\]
Solution:
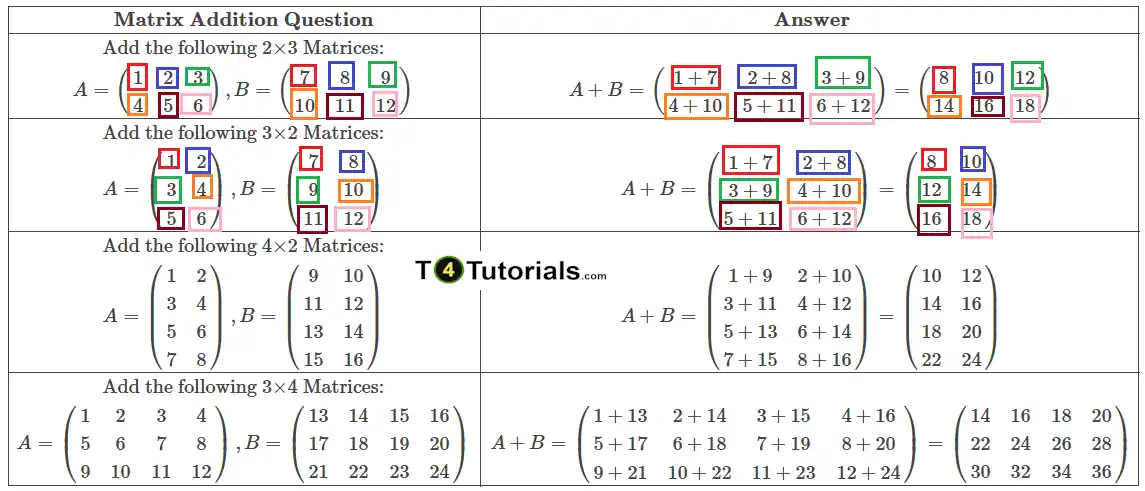
Q1: Add the following 2×3 Matrices:
A = \(\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix}\), B = \(\begin{pmatrix} 7 & 8 & 9 \\ 10 & 11 & 12 \end{pmatrix}\)
Solution:
A + B = \(\begin{pmatrix} 1+7 & 2+8 & 3+9 \\ 4+10 & 5+11 & 6+12 \end{pmatrix}\)
Result = \(\begin{pmatrix} 8 & 10 & 12 \\ 14 & 16 & 18 \end{pmatrix}\)
Q2: Add the following 3×2 Matrices:
A = \(\begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{pmatrix}\), B = \(\begin{pmatrix} 7 & 8 \\ 9 & 10 \\ 11 & 12 \end{pmatrix}\)
Solution:
A + B = \(\begin{pmatrix} 1+7 & 2+8 \\ 3+9 & 4+10 \\ 5+11 & 6+12 \end{pmatrix}\)
Result = \(\begin{pmatrix} 8 & 10 \\ 12 & 14 \\ 16 & 18 \end{pmatrix}\)
Q3: Add the following 4×2 Matrices:
A = \(\begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \\ 7 & 8 \end{pmatrix}\), B = \(\begin{pmatrix} 9 & 10 \\ 11 & 12 \\ 13 & 14 \\ 15 & 16 \end{pmatrix}\)
Solution:
A + B = \(\begin{pmatrix} 1+9 & 2+10 \\ 3+11 & 4+12 \\ 5+13 & 6+14 \\ 7+15 & 8+16 \end{pmatrix}\)
Result = \(\begin{pmatrix} 10 & 12 \\ 14 & 16 \\ 18 & 20 \\ 22 & 24 \end{pmatrix}\)
Q4: Add the following 3×4 Matrices:
A = \(\begin{pmatrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \end{pmatrix}\), B = \(\begin{pmatrix} 13 & 14 & 15 & 16 \\ 17 & 18 & 19 & 20 \\ 21 & 22 & 23 & 24 \end{pmatrix}\)
Solution:
A + B = \(\begin{pmatrix} 1+13 & 2+14 & 3+15 & 4+16 \\ 5+17 & 6+18 & 7+19 & 8+20 \\ 9+21 & 10+22 & 11+23 & 12+24 \end{pmatrix}\)
Result = \(\begin{pmatrix} 14 & 16 & 18 & 20 \\ 22 & 24 & 26 & 28 \\ 30 & 32 & 34 & 36 \end{pmatrix}\)