Site icon T4Tutorials.com

Apriori Algorithm in Data Mining with examples

Apriori Algorithm in Data Mining with examples

Apriori Helps in mining the frequent itemset.

Example of Apriori Algorithm

Let’s see an example of the Apriori Algorithm.

Minimum Support: 2

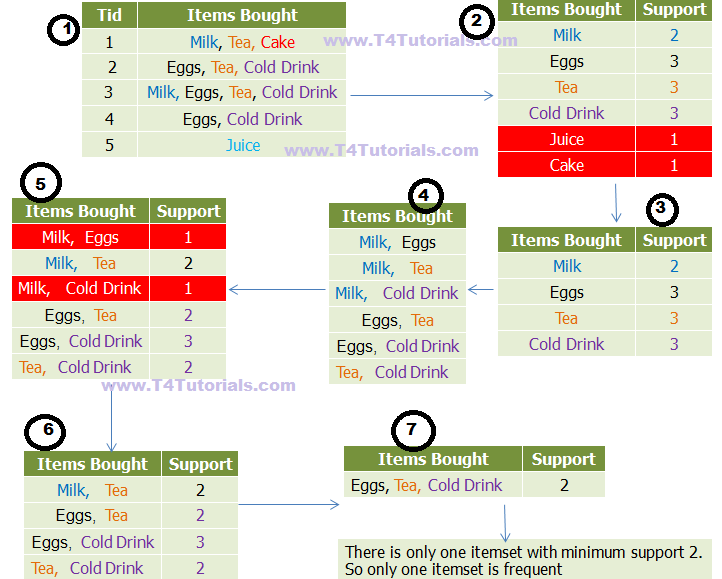
apriori in data mining

Step 1: Data in the database

Step 2: Calculate the support/frequency of all items

Step 3: Discard the items with minimum support less than 2

Step 4: Combine two items

Step 5: Calculate the support/frequency of all items

Step 6: Discard the items with minimum support less than 2

Step 6.5: Combine three items and calculate their support.

Step 7: Discard the items with minimum support less than 2

Result:

Only one itemset is frequent (Eggs, Tea, Cold Drink) because this itemset has minimum support 2 

Example 2 of Apriori Algorithm

Let’s see another example of the Apriori Algorithm.

Minimum Support :3

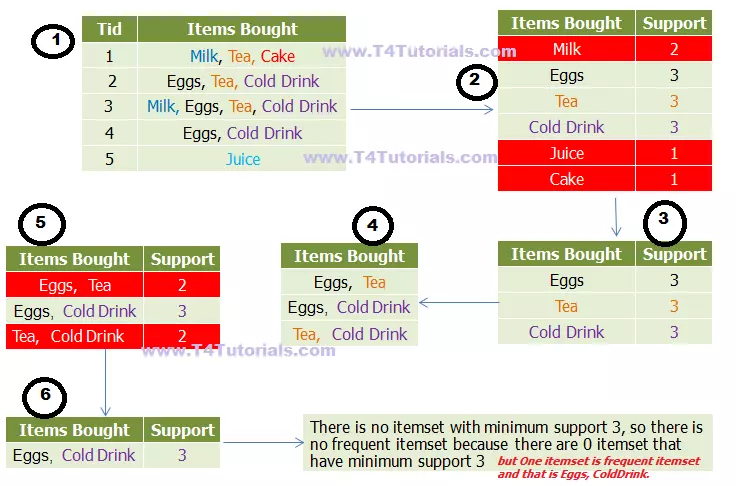
Examples of apriori alogrithm
Figure: Examples of the apriori algorithm

Step 1: Data in the database

Step 2: Calculate the support/frequency of all items

Step 3: Discard the items with minimum support less than 3

Step 4: Combine two items

Step 5: Calculate the support/frequency of all items

Step 6: Discard the items with minimum support less than 3

Step 6.5: Combine three items and calculate their support.

Step 7: Discard the items with minimum support of less than 3. So all itemsets are excluded except “Eggs, Cold drink” because this itemset has the support of 3.

Result:

There is no frequent itemset because all itemsets have minimum support of less than 3.

Advantages of  Apriori Algorithm

Apriori Algorithm is the simplest and easy to understand the algorithm for mining the frequent itemset.

Apriori Algorithm is fully supervised.

Apriori Algorithm is fully supervised so it does not require labeled data.

Apriori Algorithm is an exhaustive algorithm, so it gives satisfactory results to mine all the rules within specified confidence and sport.

Apriori principles

Downward closure property of frequent patterns

Downward closure property of frequent patterns, means that All subset of any frequent itemset must also be frequent.

Example of Downward closure property

If Notebook, Pencil, School Bag is a frequent itemset, then we can say that all of the following itemsets are frequent;

Apriori pruning principle

If an itemset is infrequent, its superset should not be generated for getting the frequent itemset.

Examples of Apriori pruning principle

If Notebook, Pencil is a frequent itemset and School Bag is not frequent itemset, then we can say that all of the following itemsets are frequent;

Apriori Candidates generation

Candidates can be generated by the self joining and Apriori pruning principles.

Step 1:

Self-joining of Apriori Candidates

Example of self-joining

A1 B1 C1 D1 E1

C1={A1 B1 C1,    A1 B1 D1,    A1 C1 D1,    A1 C1 E1,    B1 C1 D1}

Self-joining = C1 * C1A1  B1 C1 D1 from A1 B1 C1 and A1 B1 D1A1 C1  D1  E1 from A1 C1 D1 and A1 C1 E1

So frequent candidates are A1  B1 C1 D1  and A1 C1  D1  E1

Step 2: 

Apriori pruning principle

Example of Apriori pruning principle

A1 B1 C1 D1 E1C1={A1 B1 C1,    A1 B1 D1,    A1 C1 D1,    A1 C1 E1,    B1 C1 D1} According to Apriori Pruning principle A1 C1 D1 E1 is remoA1ed because A1 D1 E1 is not in C1. 

So frequent candidate is A1 B1 C1 D1

Important interview questions of  Apriori Algorithm

Let’s see some important interview questions of  Apriori Algorithm.

  1.  What are the frequent itemsets?
  2.  What is the apriori algorithm?
  3.  What is the role of the apriori algorithm in data mining?
  4.  Give some examples of the apriori algorithm in data mining.
  5.  What are the advantages of the apriori algorithm?
  6.  What are the disadvantages of the apriori algorithm?
  7.  How does the Apriori algorithm help in mining the frequent itemset?
  8.  What is Apriori pruning principle?
  9. How we can generate the Apriori candidates?
  10. What is self joining of candidates in Apriori?

Implementation of the Apriori Algorithm in C++

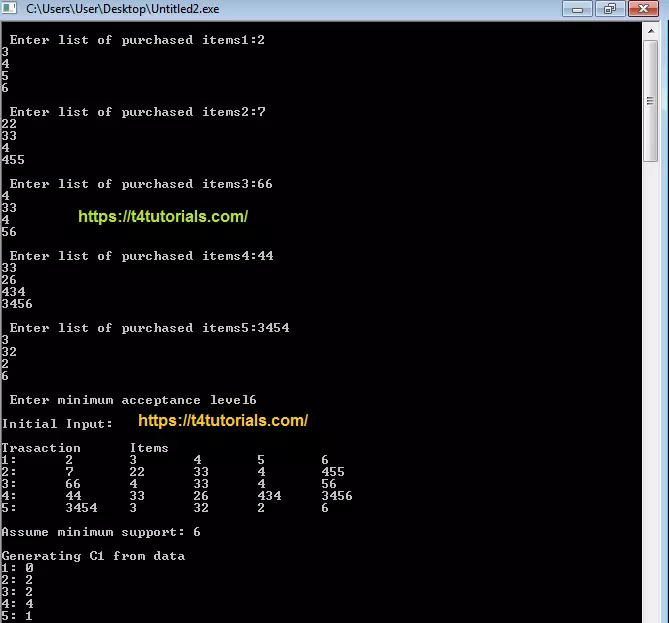
This is the demo  of Apriori algorithm  in which we are taking the list of 5 lists of purchases items and getting the result of apriori.

#include<iostream>
#include<conio.h>
using namespace std;
int main()
{
int m,i,k,l,j,t1,f;
int list1_found,list2_found,list3_found;
//Initial item-purchase
int apriori[5][5];
for(i=0;i<5;i++)
{
cout<<"\n Enter list of purchased items"<<i+1<<":"<<endl;
for(j=0;j<5;j++)
{
cin>>apriori[i][j];
}
}
//Defining minimum level for acceptence
int min;
cout<<"\n Enter minimum acceptance level"<<endl;
cin>>min;
//Printing initial input
cout<<"\nInitial Input:\n"<<endl;
cout<<"\nTrasaction\tItems\n<<endl";
for(i=0;i<5;i++)
{
cout<<i+1<<":\t";
for(j=0;j<5;j++)
{
cout<<apriori[i][j]<<"\t";
}
cout<<"\n";
}
cout<<"\nAssume minimum support: "<<min<<endl;
//First turn
int list_1[5];
for(i=0;i<5;i++)
{
t1=0;
for(j=0;j<5;j++)
{
for(k=0;k<5;k++)
{
if(apriori[j][k]==i+1)
{
t1++;
}
}
}
list_1[i]=t1;
}
//Printing first turn
cout<<"\n\nGenerating C1 from data\n"<<endl;
for(i=0;i<5;i++)
{
cout<<i+1<<": "<<list_1[i]<<"\n"<<endl;
}
//Second turn
//Counting number of possibilities for turn2
int p2pcount=0;
int list2_Purchased_Items[5];
int p2pos=0;
for(i=0;i<5;i++)
{
if(list_1[i]>=min)
{
p2pcount++;
list2_Purchased_Items[p2pos]=i;
p2pos++;
}
}
//Printing selected items for second turn
cout<<"\nGenerating LIST_1 From C1\n"<<endl;
for(i=0;i<p2pos;i++)
{
cout<<list2_Purchased_Items[i]+1<<"\t"<<list_1[list2_Purchased_Items[i]]<<"\n"<<endl;
}
//Joining items
int list2[5][3];
int firstItem2join; //will hold first item for join
int secondItem2join; //will hold second item for join
int list2pos1=0; //position pointer in list2 array
int list2ocount=0; //product join occruance counter
int list2jcount=0; //join counter
for(i=0;i<p2pcount;i++)
{
for(j=i+1;j<p2pcount;j++)
{
firstItem2join=list2_Purchased_Items[i]+1;
secondItem2join=list2_Purchased_Items[j]+1;
if(firstItem2join==secondItem2join)
{
//it is self join
continue;
}
//join the items
list2[list2pos1][0]=firstItem2join;
list2[list2pos1][1]=secondItem2join;
list2jcount++;
//count occurances
list2ocount=0; //reset counter
for(k=0;k<5;k++)
{
list1_found=list2_found=0; //resetting flag
//scan a purcahse
for(l=0;l<5;l++)
{
if(firstItem2join==apriori[k][l])
{
//one of the element found
list1_found=1;
}
if(secondItem2join==apriori[k][l])
{
//second items also found
list2_found=1;
}
}
//one purchase scanned
if(list1_found==1&&list2_found==1) //both items are present in purchase
{
list2ocount++;
}
}
//assign count
list2[list2pos1][2]=list2ocount;
list2pos1++;
}
}
//Printing second turn
cout<<"\n\nGenerating LIST2\n"<<endl;
for(i=0;i<list2jcount;i++)
{
for(j=0;j<3;j++)
{
cout<<list2[i][j]<<"\t";
}
cout<<"\n";
}
//Third turn
int p3pcount=0;
int Purchased_Items[5]={-1,-1,-1,-1,-1};
int p3pos=0;
for(i=0;i<5;i++)
{
if(list2[i][2]>=min)
{
f=0;
for(j=0;j<5;j++)
{
if(Purchased_Items[j]==list2[i][0])
{
f=1;
}
}
if(f!=1)
{
Purchased_Items[p3pos]=list2[i][0];
p3pos++;
p3pcount++;
}
f=0;
for(j=0;j<5;j++)
{
if(Purchased_Items[j]==list2[i][1])
{
f=1;
}
}
if(f!=1)
{
Purchased_Items[p3pos]=list2[i][1];
p3pos++;
p3pcount++;
}
}
}
//Joining
int list3[5][4];
int list3ocount=0; //occurance counter
int list3jcount=0; //join counter
for(i=0;i<p3pcount;i++)
{
for(j=i+1;j<p3pcount;j++)
{
for(k=j+1;k<p3pcount;k++)
{
list3[i][0]=Purchased_Items[i];
list3[i][1]=Purchased_Items[j];
list3[i][2]=Purchased_Items[k];
list3jcount++;
//count occurances
list3ocount=0; //reset counter
for(k=0;k<5;k++)
{
list1_found=list2_found=list3_found=0; //resetting flag
//scan a purcahse
for(l=0;l<5;l++)
{
if(list3[i][0]==apriori[k][l])
{
//one of the element found
list1_found=1;
}
if(list3[i][1]==apriori[k][l])
{
//second items also found
list2_found=1;
}
if(list3[i][2]==apriori[k][l])
{
//third element also found
list3_found=1;
}
}
//one purchase scanned
if(list1_found==1&&list2_found==1&&list3_found==1) //all items are present  in purchase
{
list3ocount++;
}
}
//assign count
list3[i][3]=list3ocount;
}
}
}
//Printing second turn
cout<<"\n\nGenerating LIST3\n";
for(i=0;i<list3jcount;i++)
{
for(j=0;j<4;j++)
{
cout<<list3[i][j]<<"\t";
}
cout<<"\n";
}
getch();
}

Output

implementation of apriori algoritm data mining

Video Lecture

Next Similar Tutorials

  1. Frequent pattern Mining, Closed frequent itemset, max frequent itemset in data mining – Click Here
  2. Support, Confidence, Minimum support, Frequent itemset, K-itemset, absolute support in data mining – Click Here
  3. Apriori Algorithm in Data Mining with examples – Click Here
  4. Apriori principles in data mining, Downward closure property, Apriori pruning principle – Click Here
  5. Apriori candidates’ generations, self-joining, and pruning principles. – Click Here.
Exit mobile version